题目内容
在三角形ABC中,∠A=70°,∠B,∠C的平分线交于点O,则∠BOC等于( )
| A、70° | B、125° |
| C、135° | D、110° |
考点:三角形内角和定理
专题:
分析:根据三角形的内角和定理和角平分线的定义求出∠OBC+∠OCB的度数,再根据三角形的内角和等于180°即可求出∠BOC的度数.
解答: 解:∵∠A=70°,
解:∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×110°=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
故选B.
 解:∵∠A=70°,
解:∵∠A=70°,∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-55°=125°.
故选B.
点评:本题主要利用三角形的内角和定理和角平分线的定义,熟练掌握定理和概念是解题的关键.

练习册系列答案
相关题目
 已知:如图,在半径为4的⊙O中,AB为直径,以弦AC(非直径)为对称轴
已知:如图,在半径为4的⊙O中,AB为直径,以弦AC(非直径)为对称轴 |
| AC |
A、2
| ||
B、2
| ||
C、4
| ||
| D、6 |
要锻造一个半径为5厘米,高为8厘米的圆柱毛坯,应截取半径为4厘米的圆钢( )
| A、12.5cm |
| B、13cm |
| C、13.5cm |
| D、14cm |
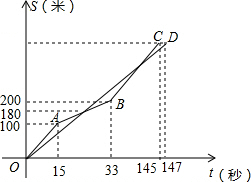 如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )| A、乙比甲先到终点 |
| B、比赛进行到29.4秒时,两人出发后第一次相遇 |
| C、乙测试的速度随时间增加而增大 |
| D、比赛全程甲的测试速度始终比乙的测试速度快 |
 我国首个空间实验室“天宫一号”顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
我国首个空间实验室“天宫一号”顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图为火箭模型的截面图,下面是梯形,中间是长方形,上面是三角形.
 如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.
如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由.