题目内容
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
 (1)求证:DE与⊙O 相切.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
(1)证明:连接BD、OD,
∵AB为⊙O的直径,∴∠ADB=∠BDC=90°,
∵E为BC边的中点,∴DE=EC,∴∠1=∠C,∵OA=OD,∴∠2=∠A,
∵∠ABC=90°,∴∠A+∠C =90°,∴∠1+∠2 =90 °,
°,
∴∠ODE =90°,∴OD⊥DE于点D,
∵以AB为直径的⊙O交AC于点D,∴D是半径的外端,
∴DE与⊙O 相切.
(2) ∵∠BDC=90°,E为BC边的中点,∴  ,∵DE=2,∴BC=4,
,∵DE=2,∴BC=4,
在Rt△ABC中,tanC= ,
,
 ∴AB=BC·
∴AB=BC· =2
=2 ,
,
在Rt△ABC中,
AC= =
= =6,
=6,
又∵△ABD∽△ACB,∴ ,
,
即 ,
,
∴AD=

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 与
与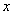 的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是
的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是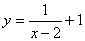 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到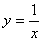 的图象,则
的图象,则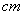 、3
、3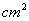 ,求
,求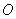 为原点,矩形
为原点,矩形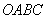 的顶点
的顶点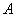 、
、 的坐标分别为(9,0)、(0,3) .点
的坐标分别为(9,0)、(0,3) .点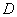 是
是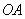 的中点,连接
的中点,连接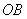 、
、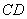 交于点
交于点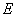 ,“反比例平移函数”
,“反比例平移函数”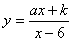 的图象经过
的图象经过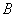 、
、 3)在(2)的条件下, 已知过线段
3)在(2)的条件下, 已知过线段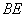 中点的一条直线
中点的一条直线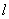 交这个“反
交这个“反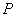 、
、 两点(
两点(

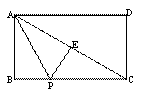
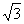 ,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是
,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是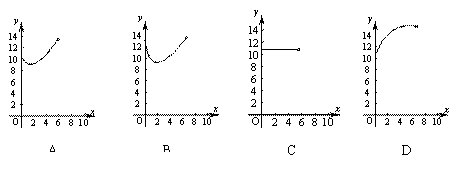
 ,求代数式
,求代数式 的值.
的值. 的绝对值是
的绝对值是 C.
C. D.
D.
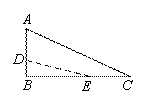 的面积S与点E运动的时间t之间的函数图象大致是
的面积S与点E运动的时间t之间的函数图象大致是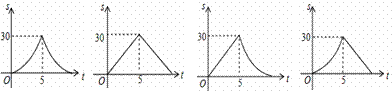
 ;
;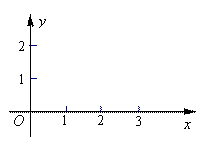
 (2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为
(2)已知:线段EF:y=x(0≤x≤3),点G到线段EF的距离d(P→EF)为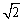 ,且点G的横坐标为1,在图2中画出图,试求点G的纵坐标.
,且点G的横坐标为1,在图2中画出图,试求点G的纵坐标.
