Question

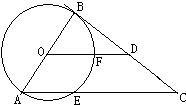13、如图，AB是⊙O的直径，BC是⊙O的切线，OD∥AC，OD、AC交⊙O与F、E，OF=AE，OA=1，那么EC=

3

．

Answer 1

分析：首先设CE=x，利用切割线定理可以得到BC²=CE•AC；再把AC用x表示出来，利用题里的已知条件和勾股定理即可列出关于x的方程，进而解方程可求出CE的长．

解答：解：∵BC是⊙O的切线，
∴BC²=CE•AC ①；
又∵BC是切线，AB是直径，
∴∠ABC=90°，
∴BC²=AC²-AB²②；
又∵OF=OA=AE=1，
∴AC=x+1，
结合①②可以得到CE•AC=AC²-AB²，
∴x（x+1）=（x+1）²-4，
∴x=3，
即EC=3．

点评：本题运用了切割线定理、勾股定理即切线的性质．解题的关键是根据前面的知识构造方程，通过解方程解决问题．