题目内容
如图(1),在平面直角坐标系中,Rt△ABC的AC边与x轴重合,且点A在原点,∠ACB=90°,∠BAC=60°,AC=2,又一直径为2的⊙D与x轴切于点E(1,0);(1)若Rt△ABC沿x轴正方向移动,当斜边AB与⊙D相切时,试写出此时点A的坐标;
(2)当Rt△ABC的边BC移动到与y轴重合时,则把Rt△ACB绕原点O按逆时针方向旋转,使斜边AB恰好经过点F(0,2),得Rt△A′B′O,AB分别与A′O、A′B′相交于M、N,如图(2)所示.
①求旋转角∠AOA′的度数;
②求四边形FOMN的面积.(结果保留根号)


【答案】分析:(1)分情况考虑:第一次和圆相切时;第二次和圆相切时.应连接圆心和切点,构造三角形求解;
(2)①容易判断出△A′OF是等边三角形,那么∠AOA'=30°;
②SFOMN=S△FOA-S△A'MN.
解答:解:(1)
当在左边相切时,∠OA′G=∠COB=60°,
∴∠DA'G=∠DA'E=60°,
∴A'E= ,此时点A坐标为(1-
,此时点A坐标为(1- ,0),
,0),
同理,当在右边相切时,A''E= ,此时点A''的坐标为(1+
,此时点A''的坐标为(1+ ,0).
,0).
综上可得A(1- ,0)或A(1+
,0)或A(1+ ,0);
,0);
(2)①∵Rt△ACB旋转得Rt△A′B′O,
∴Rt△ACB≌Rt△A′B′O.
∴∠A=∠A’=60°AO=A′O.
∵OF=OA=2,
∴△A′OF是等边三角形.
∴∠A′OF=60°.
∴∠AOA′=30°.

②在△AMO中,∠OAM=60°,∠AOA′=30°,
∴∠AMO=90°,AM= OA=
OA= ×2=1,ON=
×2=1,ON= ,MN=
,MN= ;
;
∴A′N=A′F-NF=A′O-NO=2- ,MN=
,MN= ,A′N=
,A′N= (2-
(2- );
);
∴S△A'MN= A′N•MN=
A′N•MN= (2-
(2- )2=
)2=
 -6.
-6.
过点F作FG⊥OA′于G,则FG= ,
,
∴S△FOA′= OA′•FG=
OA′•FG= ×2×
×2× =
= ;
;
∴SFOMN=S△FOA-S△A'MN= -(
-(
 -6)=6-
-6)=6-
 .
.
∴四边形FOMN的面积是(6-
 )平方单位.
)平方单位.
点评:注意分不同的情况考虑问题;判断旋转角,注意特殊角的应用是解题的关键.
(2)①容易判断出△A′OF是等边三角形,那么∠AOA'=30°;
②SFOMN=S△FOA-S△A'MN.
解答:解:(1)

当在左边相切时,∠OA′G=∠COB=60°,
∴∠DA'G=∠DA'E=60°,
∴A'E=
 ,此时点A坐标为(1-
,此时点A坐标为(1- ,0),
,0),同理,当在右边相切时,A''E=
 ,此时点A''的坐标为(1+
,此时点A''的坐标为(1+ ,0).
,0).综上可得A(1-
 ,0)或A(1+
,0)或A(1+ ,0);
,0);(2)①∵Rt△ACB旋转得Rt△A′B′O,
∴Rt△ACB≌Rt△A′B′O.
∴∠A=∠A’=60°AO=A′O.
∵OF=OA=2,
∴△A′OF是等边三角形.
∴∠A′OF=60°.
∴∠AOA′=30°.

②在△AMO中,∠OAM=60°,∠AOA′=30°,
∴∠AMO=90°,AM=
 OA=
OA= ×2=1,ON=
×2=1,ON= ,MN=
,MN= ;
;∴A′N=A′F-NF=A′O-NO=2-
 ,MN=
,MN= ,A′N=
,A′N= (2-
(2- );
);∴S△A'MN=
 A′N•MN=
A′N•MN= (2-
(2- )2=
)2=
 -6.
-6.过点F作FG⊥OA′于G,则FG=
 ,
,∴S△FOA′=
 OA′•FG=
OA′•FG= ×2×
×2× =
= ;
;∴SFOMN=S△FOA-S△A'MN=
 -(
-(
 -6)=6-
-6)=6-
 .
.∴四边形FOMN的面积是(6-

 )平方单位.
)平方单位.点评:注意分不同的情况考虑问题;判断旋转角,注意特殊角的应用是解题的关键.

练习册系列答案
相关题目
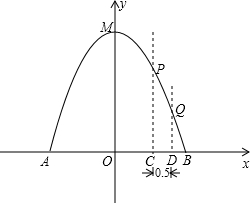 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系. 水柱在与池中心的水平距离为1m处达到最高,高度为3m.
水柱在与池中心的水平距离为1m处达到最高,高度为3m.




