题目内容
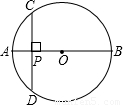
(2002•四川)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=2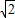 ,AB=2
,AB=2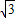 ,设∠BCD=α,那么cosα的值是( )
,设∠BCD=α,那么cosα的值是( )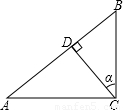
A.

B.

C.
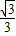
D.

【答案】分析:求出∠A=α,将求cosα的问题转化为求cos∠A的问题解答.
解答:解:∵Rt△ABC中,∠ACB=90°,CD⊥AB于D,
∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠A=∠BCD=α,
∴cosα= =
= =
= .故选D.
.故选D.
点评:此题考查了直角三角形的性质:直角三角形的两锐角互余;还考查了三角函数的定义以及转化思想.
解答:解:∵Rt△ABC中,∠ACB=90°,CD⊥AB于D,
∴∠B+∠A=90°,∠B+∠BCD=90°,
∴∠A=∠BCD=α,
∴cosα=
 =
= =
= .故选D.
.故选D.点评:此题考查了直角三角形的性质:直角三角形的两锐角互余;还考查了三角函数的定义以及转化思想.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
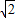 ≈1.41,
≈1.41,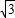 ≈1.73,
≈1.73,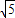 ≈2.24)
≈2.24)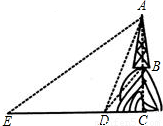


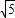 m
m