题目内容
已知:梯形ABCD,AD∥BC,E在AB上,F在DC上,且AD∥EF∥BC,AD=12cm,BC=18cm,AE:EB=2:3,则EF=________cm.

分析:延长BA和CD交于O,求出△OAD∽△OBC,求出AO:OB的值,求出OE的值,得出OE:OB的值,根据相似三角形性质即可求出答案.
解答:

解:延长BA和CD交于O,
∵AD∥BC,
∴△OAD∽△OBC,
∴
 =
= =
= =
= ,
,∴设AO=2acm,OB=3acm,
∴AB=acm,
∵AE:BE=2:3,
∴AE=
 acm,BE=
acm,BE= acm,
acm,∴OE=2acm+
 acm=
acm= acm,
acm,∵EF∥BC,
∴△OEF∽△OBC,
∴
 =
= ,
,∴
 =
= ,
,∴EF=
 (cm),
(cm),故答案为:
 .
.点评:本题考查了相似三角形的性质和判定的应用,主要考查学生的推理能力和计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
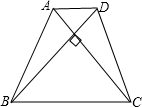 如图,已知等腰梯形ABCD的腰AB=CD=m,对角线AC⊥BD,锐角∠ABC=α,则该梯形的面积是( )
如图,已知等腰梯形ABCD的腰AB=CD=m,对角线AC⊥BD,锐角∠ABC=α,则该梯形的面积是( )| A、2msinα | B、m2(sinα)2 | C、2mcosα | D、m2(cosα)2 |
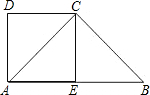 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC= 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. 4、如图,已知等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=110°,则∠BDC为( )
4、如图,已知等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=110°,则∠BDC为( )