Question

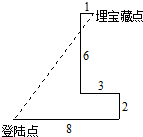暑假中，小明和同学们到某海岛去探宝旅游，按照如图所示的路线探宝．他们登陆后先往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北走6km处往东一拐，仅走1km就找到了宝藏，则登陆点到埋宝藏点的直线距离为

 

km．

Answer 1

考点：勾股定理的应用

专题：

分析：通过行走的方向和距离得出对应的线段的长度，构造直角三角形利用勾股定理求解．

解答：解：过点B作BD⊥AC于点D，
根据题意可知，AD=8-3+1=6千米，BD=2+6=8千米，
在Rt△ADB中，由勾股定理得AB=

AD2+BD2

=10千米．
答：登陆点到埋宝藏点的直线距离为10千米．
故答案为：10．

点评：本题考查了矩形的性质以及勾股定理的应用，解题的根据是结合图形，读懂题意，根据题意找到需要的数量关系，运用勾股定理求线段的长度．