题目内容
如果三条线段的长度分别为8cm、xcm、18cm,这三条线段恰好能组成一个直角三角形,那么以x为边长的正方形的面积为 .
考点:勾股定理的逆定理
专题:分类讨论
分析:本题从边的方面考查三角形形成的条件,涉及分类讨论的思考方法,即:由于“三条线段的长分别为8cm,xcm,18cm,这三条线段恰好能组成一个直角三角形”指代不明,因此,要讨论x是直角边和斜边的情形.
解答:解:当x为直角边时,18为斜边,根据勾股定理得,x2+82=182,
解得:x2=260;
当x为斜边时,根据勾股定理得,82+182=x2,
解得:x2=388.
即以xcm为边长的正方形面积是260cm2或289cm2.
故答案为260cm2或289cm2.
解得:x2=260;
当x为斜边时,根据勾股定理得,82+182=x2,
解得:x2=388.
即以xcm为边长的正方形面积是260cm2或289cm2.
故答案为260cm2或289cm2.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,线段AD的长是
如图,线段AD的长是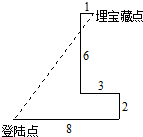 暑假中,小明和同学们到某海岛去探宝旅游,按照如图所示的路线探宝.他们登陆后先往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北走6km处往东一拐,仅走1km就找到了宝藏,则登陆点到埋宝藏点的直线距离为
暑假中,小明和同学们到某海岛去探宝旅游,按照如图所示的路线探宝.他们登陆后先往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北走6km处往东一拐,仅走1km就找到了宝藏,则登陆点到埋宝藏点的直线距离为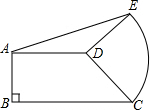 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=4,将腰CD以点D为旋转中心,逆时针方向旋转90°至点E,连接AE,请求出△ADE的面积.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=4,将腰CD以点D为旋转中心,逆时针方向旋转90°至点E,连接AE,请求出△ADE的面积.