题目内容
如图,直线 与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线
与x轴,y轴分别相交于点B,点C,经过B、C两点的抛物线 与x轴的另一交点为A,顶点为P,且对称轴是直线
与x轴的另一交点为A,顶点为P,且对称轴是直线 .
.
(1)求A点的坐标及该抛物线的函数表达式;
(2)求出∆PBC的面积;
(3)请问在对称轴 右侧的抛物线上是否存在点Q,使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的
右侧的抛物线上是否存在点Q,使得以点A、B、C、Q所围成的四边形面积是∆PBC的面积的 ?若存在,请求出点Q的坐标;若不存在,请说明理由.
?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)(1,0), .(2)3;(3)
.(2)3;(3) 或
或
解析试题分析:(1)先由直线y=-x+3与x轴,y轴分别相交于点B,点C,求出B(3,0),C(0,3),再根据抛物线y=ax2+bx+c的对称轴是直线x=2,求出与x轴的另一交点A的坐标为(1,0),然后将A(1,0),B(3,0),C(0,3)代入y=ax2+bx+c,运用待定系数法即可求出该抛物线的函数表达式;
(2)先利用配方法将二次函数写成顶点式,得到顶点P的坐标,再设抛物线的对称轴交直线y=-x+3于点M,由PM∥y轴,得出M的坐标,然后根据S△PBC= •PM•|xC-xB|即可求出△PBC的面积;
•PM•|xC-xB|即可求出△PBC的面积;
(3)设Q(m,m2-4m+3),首先求出以点A、B、C、Q所围成的四边形面积= S△PBC=
S△PBC= ×3=
×3= .再分两种情况进行讨论:①当点Q在PB段时,由S四边形ACBQ=S△ABC+S△ABQ=3+|yQ|,得出|yQ|=
.再分两种情况进行讨论:①当点Q在PB段时,由S四边形ACBQ=S△ABC+S△ABQ=3+|yQ|,得出|yQ|= -3=
-3= ,即-m2+4m-3=
,即-m2+4m-3= ,解方程求出m的值,得到Q1的坐标;②当点Q在BE段时,过Q点作QH⊥x轴,交直线于H,连结BQ.由S四边形ACQB=S△ABC+S△CBQ=3+
,解方程求出m的值,得到Q1的坐标;②当点Q在BE段时,过Q点作QH⊥x轴,交直线于H,连结BQ.由S四边形ACQB=S△ABC+S△CBQ=3+ (m2-3m),得出
(m2-3m),得出 (m2-3m)=
(m2-3m)= -3=
-3= ,解方程求出m的值,得到Q2的坐标.
,解方程求出m的值,得到Q2的坐标.
试题解析:(1)直线 与x轴相交于点
与x轴相交于点 ,
,
∴当 时,
时, ,
,
∴点 的坐标为
的坐标为 .
.
又∵抛物线过 轴
轴 两点,且对称轴为
两点,且对称轴为 ,根据抛物线的对称性,
,根据抛物线的对称性,
∴点 的坐标为
的坐标为 .
.
∵ 过点
过点 ,易知
,易知 ,
,
∴ .
.
又∵抛物线 过点
过点 ,
,
∴ 解得
解得
∴ .
.
(2)连结PB、PC,
由 ,得
,得 ,
,
设抛物线的对称轴交直线 于点
于点 ,
,
又∵PM∥y轴,则 ,
,
则
(3)由图可知,点Q应分为两种情况,在PB段或在BE段。

又
设
当点Q在PB段时, ,
,
∴ ,可知
,可知
∴ ,即
,即 ,
,
解之,得 ,
,
又点Q在对称轴的右侧,则 ,
,
∴
当点Q在BE段时,过Q作QH⊥x轴,交直线于H,连结BQ,则设
 ,
,
又 ,
,
∴ ,解之,得
,解之,得
又点Q在对称轴的右侧,则 ,
,
∴
综上所述,当 或
或

今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=- x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
(1)求出z与x的函数关系式;
(2)设第x年政府投入使用的并轨房收取的租金为W百万元,请问政府在第几年投入使用的并轨房收取的租金最多,最多为多少百万元?


 与
与 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围; 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
 表示,例如图1中,
表示,例如图1中, ,图2中,
,图2中, .
. ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: .
. ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: 中,点
中,点 ,
, 的“面积坐标”为
的“面积坐标”为 ,
, 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由; 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.
 x+m与抛物线y=
x+m与抛物线y= S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;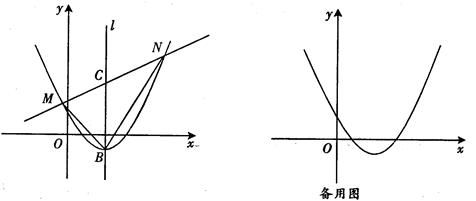
 ;
;
 的一元二次方程
的一元二次方程 .
. 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.