��Ŀ����
����1���ڡ�ABC�У�������A��B��C����ʱ�뷽�����У���涨�������Ϊ�������������������A��B��C��˳ʱ�뷽�����У���涨����������෴��Ϊ��ABC�ġ����������.������������� ��ʾ������ͼ1�У�
��ʾ������ͼ1�У� ��ͼ2�У�
��ͼ2�У� .
.
����2����ƽ������ȡһ����ABC�͵�P����P���ڡ�ABC����������ֱ���ϣ������������飨 ��
�� ��
�� ��Ϊ��P���ڡ�ABC�ġ�������ꡱ������
��Ϊ��P���ڡ�ABC�ġ�������ꡱ������ ������ͼ3�У�����ABCD�ı߳�Ϊ2��
������ͼ3�У�����ABCD�ı߳�Ϊ2�� ����
���� ����G���ڡ�ABC�ġ�������ꡱ
����G���ڡ�ABC�ġ�������ꡱ Ϊ
Ϊ .��ͼ3�У�����֪��
.��ͼ3�У�����֪�� �����á����������������Ҳ������ʽ��ʾΪ��
�����á����������������Ҳ������ʽ��ʾΪ�� .
.
Ӧ����֪��
��1����ͼ4��������ABCD�ı߳�Ϊ1���� ����D���ڡ�ABC�ġ�������ꡱ�� ��̽�����֣�
����D���ڡ�ABC�ġ�������ꡱ�� ��̽�����֣�
��2����ƽ��ֱ������ϵ �У���
���� ��
��
������P�ǵڶ�����������һ�㣨����ֱ��AB�ϣ������P���� �ġ�������ꡱΪ
�ġ�������ꡱΪ ��
��
��̽�� ��
�� ֮����������������ϵ����˵�����ɣ�
֮����������������ϵ����˵�����ɣ�
������ �ǵ�������������һ�㣬��ֱ��д����P����
�ǵ�������������һ�㣬��ֱ��д����P���� �ġ�������ꡱ����x,y��ʾ����
�ġ�������ꡱ����x,y��ʾ����
������⣺
��3���ڣ�2���������£��� ����Q��������
����Q�������� �ϣ���
�ϣ��� ��ֵ��Сʱ����Q�ĺ�����.
��ֵ��Сʱ����Q�ĺ�����.
��1��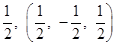 ����2����
����2����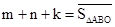 ����
����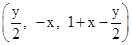 ����3��
����3��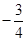 .
.
���������������1��ֱ�Ӹ��ݡ�����������͡� ������ꡱ�Ķ���д������.
��2���ٷֵ�P�ڡ�ABO�ⲿ�͵���P�ڡ�ABO�ڲ�����������ۼ���.
��ֱ�Ӹ��� �� ������ꡱ�Ķ���д������.
��3���ֵ�Q�ڵڶ����ޣ���Q�ڵ�һ���͵�Q��y��������������ۼ���.
�����������1��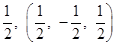 .
.
��2���ٵ���P�ڡ�ABO�ⲿʱ��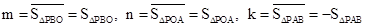 ��
��
��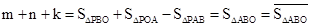 .
.
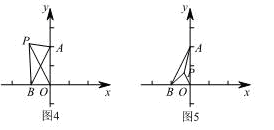
����P�ڡ�ABO�ڲ�ʱ��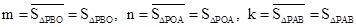 ��
��
��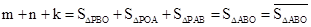 .
.
���������� .
.
��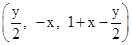 .
.
��3���ߵ�Q�������� �ϣ�����
�ϣ�����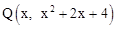 .
.
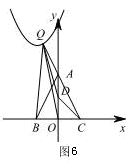
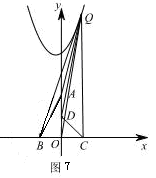
�ٵ���Q�ڵڶ�����ʱ��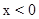 ����ͼ6��֪��
����ͼ6��֪��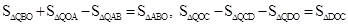 ,
,
��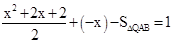 ��
��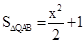 ��
��
��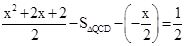 ��
��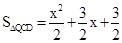 .
.
��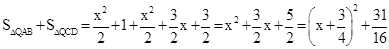 .
.
�൱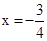 ʱ��
ʱ��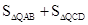 ����СֵΪ
����СֵΪ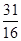 .
.
�ڵ���Q�ڵ�һ����ʱ��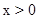 ����ͼ7��֪��
����ͼ7��֪��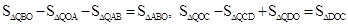 ,
,
��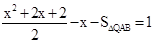 ��
��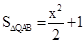 ��
��
��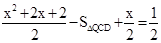 ��
��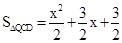 .
.
�� .
.
���ʱ��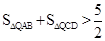 ����Сֵ.
����Сֵ.
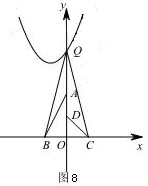
�۵���QΪ ��y��Ľ���ʱ��Q��0��4����
��y��Ľ���ʱ��Q��0��4����
��ͼ8��֪��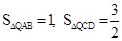 ����
����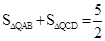 .
.
����������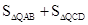 ����СֵΪ
����СֵΪ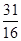 ����ʱ����Q�ĺ�����Ϊ
����ʱ����Q�ĺ�����Ϊ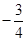 .
.
���㣺1.�¶�����Ķ��ͣ�2.������ꣻ3.���κ��������ʣ�4.����˼���Ӧ��.

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д� ͼ��A��-1��0����B��4��0�����㣮
ͼ��A��-1��0����B��4��0�����㣮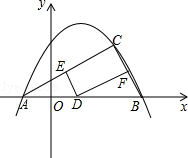

 ��������
�������� ������
������ ��0��
��0�� ����
���� ��3��4����
��3��4���� ����
���� �������߶Գ�����һ���㣬����������
�������߶Գ�����һ���㣬����������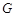 ������
������ ��ͼ��
��ͼ��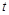 ��ȡֵ��Χ��
��ȡֵ��Χ��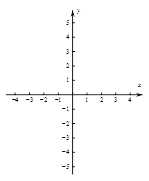
 ��x�ᣬy��ֱ��ཻ�ڵ�B����C������B��C�����������
��x�ᣬy��ֱ��ཻ�ڵ�B����C������B��C����������� ��x�����һ����ΪA������ΪP���ҶԳ�����ֱ��
��x�����һ����ΪA������ΪP���ҶԳ�����ֱ�� ��
�� �������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
 ��ͼ��x����A����1��0����B��2��0������y����C��0����2������A��C��ֱ�ߣ�
��ͼ��x����A����1��0����B��2��0������y����C��0����2������A��C��ֱ�ߣ� �����M�����꣮
�����M�����꣮
 ��������
�������� ����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8.
����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8.
 ����
���� ��
�� ��C���㣬��
��C���㣬�� ����������ֱ��
����������ֱ�� ��һ�����㣮
��һ�����㣮 ����
���� �����ֵ��
�����ֵ��
 ����������A��B��D���㣬����D��
����������A��B��D���㣬����D�� ���ƽ���߽��������ڵ�C��ֱ��l����E��0����
���ƽ���߽��������ڵ�C��ֱ��l����E��0����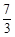 ������ƽ������ABCD�����
������ƽ������ABCD�����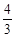 �����P�����꣮
�����P�����꣮