题目内容
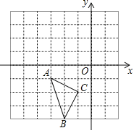
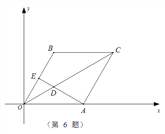
【题目】在如图直角坐标系内，四边形AOBC是边长为2的菱形，E为边OB的中点，连结AE与对角线OC交于点D，且∠BCO=∠EAO，则点D坐标为（ ）
A. （
，
） B. （1，
） C. （，） D. （1，）
【答案】D
【解析】分析：首先根据菱形的性质得出△AOD为等腰三角形，根据菱形的性质得出∠BOA=2∠AOE，结合AO=2OE得出△AOD为底角为30°角的等腰三角形，从而得出点D的坐标．
详解：∵BC∥OA， ∴∠BCO=∠COA， 又∵∠BCO=∠EAO， ∴∠COA=∠EAO，
∴△AOD为等腰三角形， ∴点D的横坐标为1， ∵四边形OACB为菱形，
∴∠BOA=2∠AOE， ∵AO=2OE， ∴∠DAO=∠DOA=30°，
∴点D的纵坐标为
， ∴点D的坐标为(1，)．故选D．
练习册系列答案
阅读快车系列答案
相关题目
【题目】甲、乙二人同时从学校出发，沿同一方向匀速行走，
后，甲加快速度继续匀速行走(加速的时间忽略不计)，乙始终匀速行走，两人都走了
.两人在行走过程中得到如下表所示的信息：
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
（1）根据题意，甲出发时的速度为_______
，乙的速度为______；
（2）求表中
的值．
