题目内容
 19、如图所示,折叠长方形(四个角都是直角,)的一边AD使点D落在BC边的点F处,已知AB=DC=8cm,AD=BC=10cm,求EC的长.
19、如图所示,折叠长方形(四个角都是直角,)的一边AD使点D落在BC边的点F处,已知AB=DC=8cm,AD=BC=10cm,求EC的长.分析:想求得EC长,利用勾股定理计算,需求得FC长,那么就需求出BF的长,利用勾股定理即可求得BF长.
解答:解:设EC的长为xcm,(1分)
∴DE=(8-x)cm.(2分)
∵△ADE折叠后的图形是△AFE,
∴AD=AF,∠D=∠AFE,DE=EF.(3分)
∵AD=BC=10cm,
∴AF=AD=10cm.(4分)
又∵AB=8cm,在RT△ABF中,根据勾股定理,得AB2+BF2=AF2
∴82+BF2=102(5分)
∴BF=6cm.(6分)
∴FC=BC-BF=10-6=4cm.(7分)
在RT△EFC中,根据勾股定理,得:FC2+EC2=EF2
∴42+x2=(8-x)2(8分)即16+x2=64-16x+x2,
化简,得16x=48.(9分)
∴x=3.
故EC的长为3cm.(10分)
∴DE=(8-x)cm.(2分)
∵△ADE折叠后的图形是△AFE,
∴AD=AF,∠D=∠AFE,DE=EF.(3分)
∵AD=BC=10cm,
∴AF=AD=10cm.(4分)
又∵AB=8cm,在RT△ABF中,根据勾股定理,得AB2+BF2=AF2
∴82+BF2=102(5分)
∴BF=6cm.(6分)
∴FC=BC-BF=10-6=4cm.(7分)
在RT△EFC中,根据勾股定理,得:FC2+EC2=EF2
∴42+x2=(8-x)2(8分)即16+x2=64-16x+x2,
化简,得16x=48.(9分)
∴x=3.
故EC的长为3cm.(10分)
点评:翻折中较复杂的计算,需找到翻折后相应的直角三角形,利用勾股定理求解所需线段.

练习册系列答案
相关题目
 如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为
如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为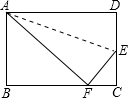 (1)计算:
(1)计算: 29、如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求FC和EF的长.
29、如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求FC和EF的长. 如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求BF与FC的长.
如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求BF与FC的长.