题目内容
（1）计算：| a2-1 |
| a2-2a+1 |
| 2a-a2 |
| a-2 |
（2）解分式方程：
| x |
| x+2 |
| x+2 |
| x-2 |
| 8 |
| x2-4 |
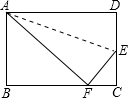
（3）已知，如图所示，折叠长方形的一边AD，使点D落在BC边的点F处，如果AB=8cm，BC=10cm，求EC的长．
分析：（1）利用完全平方公式（a±b）2=a2±2ab+b2，化简；
（2）先去分母，反分式方程化为整式方程后，求解，要验根；
（3）根据折叠的性质知，DE=EF=CD-CE，AD=AF=BC=10cm，在Rt△ABF中，由勾股定理得到BF=
=6cm，在Rt△EFC中，CE2+FC2=EF2，化简后求解得到EC的值．
（2）先去分母，反分式方程化为整式方程后，求解，要验根；
（3）根据折叠的性质知，DE=EF=CD-CE，AD=AF=BC=10cm，在Rt△ABF中，由勾股定理得到BF=
| AF2-AB2 |
解答：解：（1）
+
÷a=
+
•
=
-1
=
=
；
（2）方程两边同乘以（x+2）（x-2），去分母得：
x（x-2）-（x+2）2=8
化简得：x2-2x-x2-4x-4=8
-6x=8+4
解得：x=-2
检验：把x=-2代入（x+2）（x-2）=0，x=-2是增根．
所以原分式方程无解；
（3）由题意知：△ADE≌△AFE，
∴AD=AF，DE=EF．
∵四边形ABCD是矩形，
∴AD=AF=BC=10cm，DC=AB=8cm，∠B=∠C=90°，
在Rt△ABF中，BF=
=6cm，
∴FC=4cm，
设CE=xcm，则DE=EF=（8-x）cm，
在Rt△EFC中，CE2+FC2=EF2，
即x2+42=（8-x）2解得：x=3．
即CE=3cm．
| a2-1 |
| a2-2a+1 |
| 2a-a2 |
| a-2 |
| (a-1)(a+1) |
| (a-1)2 |
| -a(a-2) |
| (a-2) |
| 1 |
| a |
=
| a+1 |
| a-1 |
=
| a+1-a+1 |
| a-1 |
=
| 2 |
| a-1 |
（2）方程两边同乘以（x+2）（x-2），去分母得：
x（x-2）-（x+2）2=8
化简得：x2-2x-x2-4x-4=8
-6x=8+4
解得：x=-2
检验：把x=-2代入（x+2）（x-2）=0，x=-2是增根．
所以原分式方程无解；
（3）由题意知：△ADE≌△AFE，
∴AD=AF，DE=EF．
∵四边形ABCD是矩形，
∴AD=AF=BC=10cm，DC=AB=8cm，∠B=∠C=90°，
在Rt△ABF中，BF=
| AF2-AB2 |
∴FC=4cm，
设CE=xcm，则DE=EF=（8-x）cm，
在Rt△EFC中，CE2+FC2=EF2，
即x2+42=（8-x）2解得：x=3．
即CE=3cm．
点评：本题利用了：1、折叠的性质：折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；2、勾股定理，矩形的性质；3、完全平方公式化简代数式；4、去分母解分式方程．
练习册系列答案
相关题目