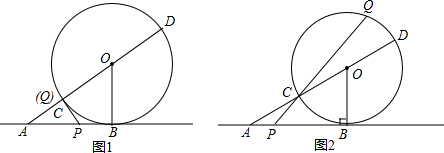题目内容
8.如图①、②,∠ABC=90°,D是线段AB延长线的点,AD=BC.探究:如图①,过点A作AF⊥AB,F、C在直线AB的两侧,截取AF=BD,连结DC、DF、CF.求证:DF=DC,∠FDC=90°.
应用:如图②,E是线段BC延长线上一点,直线AE、CD相交于点P,若CE=BD,则∠APD的大小为45度.
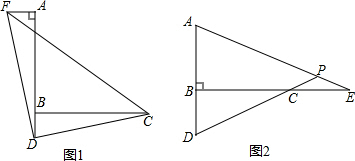
分析 (1)由已知证明△FAD≌△DBC,得到DF=DC,∠FDA=∠DCB,由∠DCB+∠BDC=90°,得到∠FDA+∠BDC=90°,所以∠FDC=90°;
(2)过点A作AF⊥AB,并截取AF=BD,连接DF、CF,证明四边形AFCE为平行四边形,得到FC∥AE,得到∠APD=∠FCD,根据∠FCD=45°,所以∠APD=45°.
解答 解:(1)∵∠ABC=90°,AF⊥AB,
∴∠FAD=∠DBC=90°,
在△FAD和△DBC中,
$\left\{\begin{array}{l}{AD=BC}\\{∠FAD=∠DBC}\\{AF=BD}\end{array}\right.$
∴△FAD≌△DBC,
∴DF=DC,∠FDA=∠DCB,
∵∠DCB+∠BDC=90°,
∴∠FDA+∠BDC=90°,
∴∠FDC=90°.
(2)如图2,过点A作AF⊥AB,并截取AF=BD,连接DF、CF,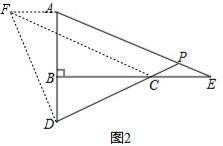
∵∠ABC=90°,AF⊥AB,
∴AF∥CE,
∵AF=BD,CE=BD,
∴AF=CE,
∴四边形AFCE是平行四边形,
∴FC∥AE,
∴∠APD=∠FCD,
∵DF=DC,∠FDC=90°.
∴∠FCD=45°,
∴∠APD=45°.
故答案为:45.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是作出辅助线,得出四边形AFCE为平行四边形.

练习册系列答案
相关题目
19.若a+b<0,ab<0,则a,b两数应该是( )
| A. | a,b两数同正 | B. | a,b异号且负数的绝对值大 | ||
| C. | a,b两数同负 | D. | a,b异号且正数的绝对值大 |
18.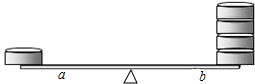 如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
(1)根据统计记录,你发现的规律是a=nb;
(2)若直尺长60cm,直尺的一端放一枚棋子,另一端放9枚棋子,试用一元一次方程求出a,b的值.
 如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:
如图,用一根质地均匀的直尺和一些棋子做实验:在直尺的一端放一枚棋子.另一端放n枚棋子,移动质点的位置,使两边平衡,记录支点到两端的距离a,b,如下表:| n(枚) | 1 | 2 | 3 | 4 | 5 |
| a/cm | 15 | 20 | 22.5 | 24 | 25 |
| b/cm | 15 | 10 | 7.5 | 6 | 5 |
(2)若直尺长60cm,直尺的一端放一枚棋子,另一端放9枚棋子,试用一元一次方程求出a,b的值.