题目内容
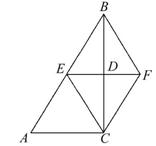
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF
C.BD=DF D.AC=BF
 ‘
‘
D.∵EF垂直平分BC,
∴BE=EC,BF =CF,
=CF,
∵BF=BE,∴BE=EC=CF=BF,
∴四边形BECF是菱形.
当BC=AC时,∵∠ACB=90°,则∠A=45°.
∵∠A=45°,∠ACB=90°,∴∠EBC=45°.
∴∠EBF=2∠EBC=2×45°=90°,
∴菱形BECF是正方形.
当CF⊥BF时,利用正方形的判定定理得出,菱形BECF是正方形;
当BD=DF时,利用正方形的判定得出,菱形BECF是正方形;
当AC=BF时,无法得出菱形BECF是正方形,故选项D符合题意.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 .
. =11;同样1112=12321,
=11;同样1112=12321, =111;…,由此猜想
=111;…,由此猜想 =
=  .
.


 的线段的概率为( )
的线段的概率为( ) B.
B. C.
C. D.
D.

 .
. 都有公共点;
都有公共点;
 可因式分解为
可因式分解为 ,则
,则 、
、 的值为( ).
的值为( ). B.
B. C.
C. D.
D.