题目内容
12. 如图,在⊙O中,弦AB=AC,AD是⊙O的直径,试判断弦BD和CD是否相等,并说明理由.
如图,在⊙O中,弦AB=AC,AD是⊙O的直径,试判断弦BD和CD是否相等,并说明理由.
分析 根据AB=AC,得到$\widehat{AB}$=$\widehat{AC}$,于是得到∠ADB=∠ADC,根据AD是⊙O的直径,得到∠B=∠C=90°,根据三角形的内角和定理得到∠BAD=∠DAC,于是得到结论.
解答 解:∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴∠ADB=∠ADC,
∵AD是⊙O的直径,
∴∠B=∠C=90°,
∴∠BAD=∠DAC,
∴$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD.
点评 本题考查了圆周角定理,熟记圆周角定理是解题的关键.

练习册系列答案
相关题目
7.已知点(-1,y1),(2,y2),(-3,y3)都在函数y=x2的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
4. 如图,在△ABC中,AD⊥BC于点D,DE⊥AB于点E,则图中一定相似的三角形有( )
如图,在△ABC中,AD⊥BC于点D,DE⊥AB于点E,则图中一定相似的三角形有( )
 如图,在△ABC中,AD⊥BC于点D,DE⊥AB于点E,则图中一定相似的三角形有( )
如图,在△ABC中,AD⊥BC于点D,DE⊥AB于点E,则图中一定相似的三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
1.已知二次函数y=ax2,下列说法不正确的是( )
| A. | 对称轴为y轴 | B. | 当a<0,x≠0时,y轴总为负值 | ||
| C. | 当a>0时,y有最小值0 | D. | 当a<0,x<0时,y随x的增大而减小 |
 如图,已知△ABC,在图中画出:
如图,已知△ABC,在图中画出: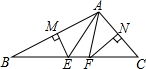 已知:如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、E,AC的垂直平分线分别交AC、BC于点N、F,∠B=27°,∠BAC=2∠C.求∠EAF的度数.
已知:如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、E,AC的垂直平分线分别交AC、BC于点N、F,∠B=27°,∠BAC=2∠C.求∠EAF的度数. 如图所示,∠B=∠C=90°,M为BC的中点,AM平分∠DAB.求证:
如图所示,∠B=∠C=90°,M为BC的中点,AM平分∠DAB.求证: