题目内容
 如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,则:
如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,则:
(1)汽车行使前油箱里有______L汽油.
(2)油箱中剩油y(L)与行使时间x(h)之间的函数关系是______,自变量取值范围为______.
解:(1)根据图象可得出:当x=0时,则y=40,
故答案为:40;
(2)设油箱中剩油y(L)与行使时间x(h)之间的函数关系为y=kx+b(k≠0),
把(0,40)、(8,0)代入得:
 ,
,
解得:
 ,
,
∴y与x的函数关系式为y=-5x+40;
油箱中剩油y(L)与行使时间x(h)之间的函数关系为y=-5x+40.
当x=0时,则y=40;
当y=0时,则-5x+40=0,
解得x=8,
故自变量取值范围为:0≤x≤8.
故答案为:y=-5x+40,0≤x≤8.
分析:(1)求汽车行使前油箱里的汽油量,就是求x=0时的函数值;
(2)根据函数图象横坐标即可得出x的取值范围,利用待定系数法确定解析式.
点评:本题考查了一次函数的应用:先利用待定系数法确定一次函数关系式,然后根据一次函数的性质解决实际问题;学会把函数图象中的有关数与实际中的数据对应起来.
故答案为:40;
(2)设油箱中剩油y(L)与行使时间x(h)之间的函数关系为y=kx+b(k≠0),
把(0,40)、(8,0)代入得:
 ,
,解得:
 ,
,∴y与x的函数关系式为y=-5x+40;
油箱中剩油y(L)与行使时间x(h)之间的函数关系为y=-5x+40.
当x=0时,则y=40;
当y=0时,则-5x+40=0,
解得x=8,
故自变量取值范围为:0≤x≤8.
故答案为:y=-5x+40,0≤x≤8.
分析:(1)求汽车行使前油箱里的汽油量,就是求x=0时的函数值;
(2)根据函数图象横坐标即可得出x的取值范围,利用待定系数法确定解析式.
点评:本题考查了一次函数的应用:先利用待定系数法确定一次函数关系式,然后根据一次函数的性质解决实际问题;学会把函数图象中的有关数与实际中的数据对应起来.

练习册系列答案
相关题目
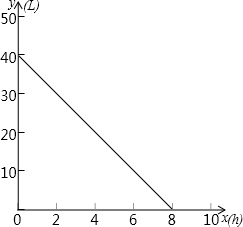 如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题:
如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题: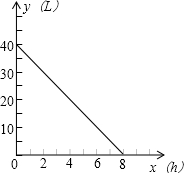 如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,则:
如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,则: 如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题.
如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题. 如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题:
如图是一辆汽车油箱里剩油量y(L)与行驶时间x(h)的图象,根据图象回答下列问题: