题目内容
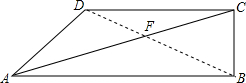如图，四边形ABCD中，∠B=90°，DC∥AB，AC平分∠BAD，∠DAB=30°，求证：AD=2BC．考点：含30度角的直角三角形
专题：证明题
分析：过D作DE⊥AB交AB于点E，则可证得EBCD为平行四边形，可得DE=BC，在Rt△ADE中，由直角三角形的性质可得出结论．
解答：
证明：
过D作DE⊥AB交AB于点E，
∵∠B=∠DEA=90°，
∴BC∥DE，
∵DC∥AB，
∴四边形BCDE为平行四边形，
∴BC=DE，
在Rt△ADE中，
∵∠DAB=30°，
∴AD=2DE，
∴AD=2BC．
证明：
过D作DE⊥AB交AB于点E，
∵∠B=∠DEA=90°，
∴BC∥DE，
∵DC∥AB，
∴四边形BCDE为平行四边形，
∴BC=DE，
在Rt△ADE中，
∵∠DAB=30°，
∴AD=2DE，
∴AD=2BC．
点评：本题主要考查直角三角形的性质，利用条件得出DE和BC的关系是解题的关键．
练习册系列答案
相关题目
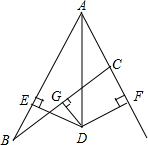如图，在△ABC中，AD平分∠BAC，DG⊥BC且平分BC于点G，DE⊥AB于E，DF⊥AC于F．
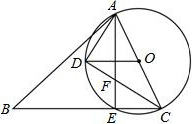如图，在锐角△ABC中，AC是最短边，以AC中点O为圆心，AC为直径作⊙O，交BC于点E，过O作OD∥BC交⊙O于点D，连结AE，AD，DC．求证：