题目内容
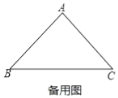
【题目】如图乙,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
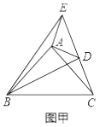
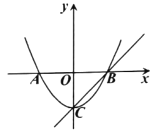
(1)如图甲,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 、
、![]() 、
、![]() 在同一条直线上时,连接
在同一条直线上时,连接![]() 、
、![]() ,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
,则下列给出的四个结论中,其中正确的是哪几个 ;(回答直接写序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
(2)若![]() ,
,![]() ,把
,把![]() 绕点
绕点![]() 旋转.
旋转.
①当![]() 时,求
时,求![]() 的长;
的长;
②直接写出旋转过程中线段![]() 的最大值和最小值.
的最大值和最小值.
【答案】(1)①②③;(2)①![]() 或
或![]() ;②
;②![]() 长的最小值是
长的最小值是![]() ,最大值是
,最大值是![]() .
.
【解析】
(1)①由条件证明△ABD≌△ACE,就可以得到结论②由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°,进而得出结论;③由条件知∠ABC=∠ABD+∠DBC=45°,由∠ABD=∠ACE就可以得出结论;④△BDE为直角三角形就可以得出BE2=BD2+DE2,由△DAE和△BAC是等腰直角三角形就有DE2=2AD2,BC2=2AB2,就有BC2=BD2+CD2≠BD2就可以得出结论.
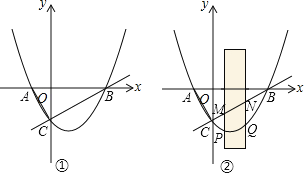
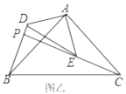
(2)①分两种情形a、如图2中,当点E在AB上时,BE=AB-AE=3,由△PEB∽△AEC,得![]() ,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=9,解法类似;
,由此即可解决问题.b、如图3中,当点E在BA延长线上时,BE=9,解法类似;
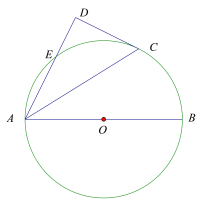
②a、如图4中,以A为圆心AD为半径画圆,当CE在⊙A上方与⊙A相切时,PB的值最大.b、如图5中,以A为圆心AD为半径画圆,当CE在⊙A下方与⊙A相切时,PB的值最小,分别求出PB即可.
(1)解:如图甲: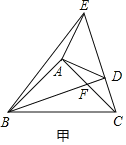
①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
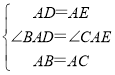 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,∴①正确;
②∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠CAB=90°,
∴∠ABD+∠AFB=90°,
∴∠ACE+∠AFB=90°.
∵∠DFC=∠AFB,
∴∠ACE+∠DFC=90°,
∴∠FDC=90°.
∴BD⊥CE,∴②正确;
③∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ABD+∠DBC=45°.
∴∠ACE+∠DBC=45°,∴③正确;
④∵BD⊥CE,
∴BE2=BD2+DE2,
∵∠BAC=∠DAE=90°,AB=AC,AD=AE,
∴DE2=2AD2,BC2=2AB2,
∵BC2=BD2+CD2≠BD2,
∴2AB2=BD2+CD2≠BD2,
∴BE2≠2(AD2+AB2),∴④错误.
故答案为①②③.
(2)①解:a.如图2中,当点![]() 在
在![]() 上时,
上时,![]() .
.
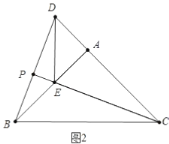
∵![]() ,
,
∴![]() ,
,
同(1)可证![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
b.如图3中,当点![]() 在
在![]() 延长线上时,
延长线上时,![]() ,
,
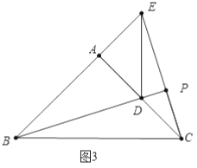
∵![]() ,
,
∴![]() ,
,
同(1)可证![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,综上,
,综上,![]() 或
或![]() ;
;
②解:a.如图4中,以![]() 为圆心
为圆心![]() 为半径画圆,当
为半径画圆,当![]() 在
在![]() 下方与
下方与![]() 相切时,
相切时,![]() 的值最小.
的值最小.
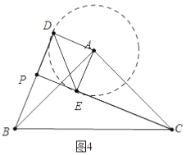
理由:此时![]() 最小,由(1)可知
最小,由(1)可知![]() 是直角三角形,斜边
是直角三角形,斜边![]() 为定值,
为定值,![]() 最小,因此
最小,因此![]() 最小,
最小,
∵![]() ,
,
∴![]() ,
,
由(1)可知,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,且AD=AE=3,
,且AD=AE=3,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ;
;
b.如图5中,以![]() 为圆心
为圆心![]() 为半径画圆,当
为半径画圆,当![]() 在
在![]() 上方与
上方与![]() 相切时,
相切时,![]() 的值最大.
的值最大.
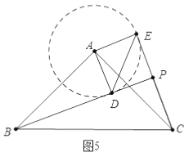
理由:此时![]() 最大,因此
最大,因此![]() 最大,(同理,
最大,(同理,![]() 是直角三角形,斜边
是直角三角形,斜边![]() 为定值,
为定值,![]() 最大,因此
最大,因此![]() 最大)
最大)
∵![]() ,
,
∴![]() ,
,
由(1)可知,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,且AD=AE=3,
,且AD=AE=3,
∴四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() .
.
综上所述,![]() 长的最小值是
长的最小值是![]() ,最大值是
,最大值是![]() .
.