题目内容
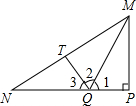如图，MP⊥NP，MQ为△NMP的角平分线，MT=MP，连结TQ，则下列结论中，不一定正确的是（ ）| A、TQ=PQ |
| B、∠1=∠2 |
| C、∠QTN=90° |
| D、∠2=∠3 |
考点：角平分线的性质,全等三角形的判定与性质
专题：
分析：根据角平分线的定义可得∠QMT=∠QMP，然后利用“边角边”证明△QMT和△QMP全等，根据全等三角形对应边相等可得TQ=PQ，全等三角形对应角相等可得∠1=∠2，∠QTN=∠P=90°．
解答：解：∵MQ为△NMP的角平分线，
∴∠QMT=∠QMP，
在△QMT和△QMP中，
，
∴△QMT≌△QMP（SAS），
∴TQ=PQ，∠1=∠2，∠QTN=∠P=90°，
∴结论不一定正确的是∠2=∠3．
故选D．
∴∠QMT=∠QMP，
在△QMT和△QMP中，
|
∴△QMT≌△QMP（SAS），
∴TQ=PQ，∠1=∠2，∠QTN=∠P=90°，
∴结论不一定正确的是∠2=∠3．
故选D．
点评：本题考查了角平分线的性质，全等三角形的判定与性质，求出三角形全等是解题的关键．
练习册系列答案
相关题目
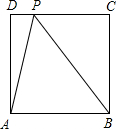如图，正方形ABCD的边长为4，动点P从D出发以1个单位每秒的速度往C运动，动点Q从A出发以3个单位每秒的速度经B往C运动，若P、Q同时出发，其中一个点运动到C时，另一点也随即停止运动，连结PA、PQ，若记△APQ的面积为y，运动时间为x秒．