题目内容
7．
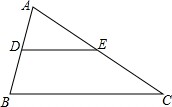如图，在△ABC中，点D、E分别在AB、AC上，且DE∥BC．（1）求证：△ADE∽△ABC；
（2）若AD：DB=2：3，AC=10，求AE长．
分析 （1）根据DE与BC平行得到对应角相等，从而证明所求的两三角形相似；
（2）根据平行线分相等成比例，得到比例式，代入数据即可得到结论．
解答 （1）证明：∵DE∥BC，
∴∠B=∠ADE，∠C=∠AED，
∴△ABC∽△ADE；
（2）解：∵DE∥BC，
∴$\frac{AD}{AB}=\frac{AE}{AC}$，
∵AD：DB=2：3，AC=10，
∴$\frac{2}{5}=\frac{AE}{10}$，
∴AE=4．
点评 本题考查了相似三角形的性质，平行线分相等成比例，熟练掌握相似三角形的性质是解题的关键．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
的整数部分为m，小数部分为n，求
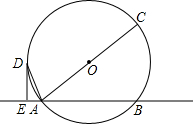如图，直线EF交⊙O于A，B两点，AC是⊙O直径，DE是⊙O的切线，且DE⊥EF，垂足为E．
如图，已知四边形DEFG是△ABC的内接正方形，S△ADG=1，S△CFG=1，S△BDE=3，求△ABC的面积．