题目内容
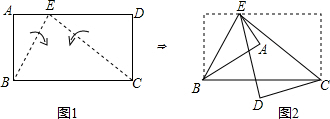 如图,在矩形ABCD中,E点在AD上,并且BE=2AE,分别以BE、CE为折线,将A、D向BC的方向折叠,对折后A、B、C、D、E五点在同一平面上.若∠AED=n°,则∠BCE的度数为
如图,在矩形ABCD中,E点在AD上,并且BE=2AE,分别以BE、CE为折线,将A、D向BC的方向折叠,对折后A、B、C、D、E五点在同一平面上.若∠AED=n°,则∠BCE的度数为考点:翻折变换(折叠问题)
专题:
分析:由题意BE=2AE=2A′E,∠A=∠A′=90°,即可得△ABE、△A′BE皆为30°、60°、90° 的三角形,然后可求得∠AED′的度数,又由∠AED=n°,即可求得∠DED′的度数,继而求得∠BCE=∠2的度数.
解答: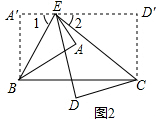 解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
∴△ABE、△A′BE皆为30°、60°、90° 的三角形,
∴∠1=∠AEB=60°,
∴∠AED′=180°-∠1-∠AEB=180°-60°-60°=60°,
∴∠DED′=∠AED+∠AED′=n°+60°=(n+60)°,
∴∠2=
∠DED′=(
n+30)°,
∵A′D′∥BC,
∴∠BCE=∠2=(
n+30)°.
故答案为:(
n+30).
 解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,
解:根据题意得:∵BE=2AE=2A′E,∠A=∠A′=90°,∴△ABE、△A′BE皆为30°、60°、90° 的三角形,
∴∠1=∠AEB=60°,
∴∠AED′=180°-∠1-∠AEB=180°-60°-60°=60°,
∴∠DED′=∠AED+∠AED′=n°+60°=(n+60)°,
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
∵A′D′∥BC,
∴∠BCE=∠2=(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:此题考查了翻折变换的性质、矩形的性质以及含30°角的直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意折叠中的对应关系.

练习册系列答案
相关题目
不等式1-2x<5-
x的负整数解有( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 投掷一枚质地均匀的正方体骰子.
投掷一枚质地均匀的正方体骰子.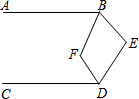 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=110°,则∠BFD的度数为
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=110°,则∠BFD的度数为 如图,△ABC中,已知AB=8,BC=6,CA=4,D、E分别是AB、AC边的中点,则DE=
如图,△ABC中,已知AB=8,BC=6,CA=4,D、E分别是AB、AC边的中点,则DE= 如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为8cm,则MN的长为
如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为8cm,则MN的长为