题目内容
 如图,已知AD=DB=BC,如果∠C=α,那么∠ABC=________.
如图,已知AD=DB=BC,如果∠C=α,那么∠ABC=________.
180°-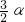
分析:根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可推出∠BDC与∠BDA的关系,从而不难求解.
解答:∵AD=DB=BC,∠C=α
∴∠A=∠DBA,∠BDC=∠C=α
∵∠BDC=∠A+∠DBA
∴∠DBA=
∴∠ABC=∠DBA+∠DBC= +(180°-2α)=180°-
+(180°-2α)=180°-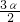 .
.
故答案为:180°-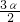 .
.
点评:此题主要考查等腰三角形的性质,三角形内角和定理及三角形外角的性质的综合运用.
分析:根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可推出∠BDC与∠BDA的关系,从而不难求解.
解答:∵AD=DB=BC,∠C=α
∴∠A=∠DBA,∠BDC=∠C=α
∵∠BDC=∠A+∠DBA
∴∠DBA=

∴∠ABC=∠DBA+∠DBC=
 +(180°-2α)=180°-
+(180°-2α)=180°-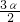 .
.故答案为:180°-
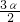 .
.点评:此题主要考查等腰三角形的性质,三角形内角和定理及三角形外角的性质的综合运用.

练习册系列答案
相关题目
 如图,已知AD=DB,CD⊥AB,E是BC延长线上一点,∠A=36°,则∠DCE=
如图,已知AD=DB,CD⊥AB,E是BC延长线上一点,∠A=36°,则∠DCE= 如图,已知AD=DB=BC,如果∠C=α,那么∠ABC=
如图,已知AD=DB=BC,如果∠C=α,那么∠ABC= 20、如图:已知AD=DB=BC,∠C=25°,则∠ADE=
20、如图:已知AD=DB=BC,∠C=25°,则∠ADE= 如图,已知AD=DB=BC,∠C=50°,则∠ABC=
如图,已知AD=DB=BC,∠C=50°,则∠ABC= DB,E是BC的中点,BE=
DB,E是BC的中点,BE= AC=2cm,求线段DE的长.
AC=2cm,求线段DE的长.