题目内容
16. 如图,在直角三角形ABC中,∠ACB=90°,CD是AB上的高,AC=4,BC=3,如果圆C是以C为圆心,2.5长为半径的圆,那么下列说法正确的是( )
如图,在直角三角形ABC中,∠ACB=90°,CD是AB上的高,AC=4,BC=3,如果圆C是以C为圆心,2.5长为半径的圆,那么下列说法正确的是( )| A. | 点D在圆C上 | B. | 点D在圆C内,点A、B均在圆C外 | ||
| C. | 点A、B、D均在圆C外 | D. | 点B、D均在圆C内,点A在圆C外 |
分析 先根据勾股定理求出AB的长,再由三角形的面积公式求出CD的长,根据点与圆的位置关系即可得出结论.
解答 解:∵在直角三角形ABC中,∠ACB=90°,CD是AB上的高,AC=4,BC=3,
∴AB=$\sqrt{{AC}^{2}+{BC}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴CD=$\frac{AC•BC}{AB}$=$\frac{4×3}{5}$=$\frac{12}{5}$=2.4.
A、∵2.4<2.5,∴点D在圆内,故本选项错误;
B、∵2.4<2.5<3<4,∴点D在圆C内,点A、B均在圆C外,故本选项正确;
C、∵2.4<2.5,∴点D在圆内,故本选项错误;
D、∵2.4<2.5<3<4,∴点D在圆C内,点A、B均在圆C外,故本选项错误.
故选B.
点评 本题考查的是点与圆的位置关系,根据三角形的面积公式求出CD的长是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某校对初二年级1600名男生的身高进行了测量,结果身高(单位:m)在1.58~1.65这一小组的频率为0.4,则该组的人数为( )
| A. | 640人 | B. | 480人 | C. | 400人 | D. | 40人 |
8. 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A. | 5 | B. | 10 | C. | 6 | D. | 8 |

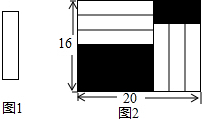 把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是64cm.
把六张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为20cm,宽为16cm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分周长的和是64cm.