题目内容
如图，已知AC、BD是圆内接四边形ABCD的两条对角线，且AB=BC，过B作一弦BE交AC于点F．（1）图中与∠ADB相等的角有哪些？
（2）试说明：BC2=BE•BF．
考点：圆周角定理,相似三角形的判定与性质
专题：证明题
分析：（1）根据同圆中等弧或同弧所对的圆周角相等，即可求解；
（2）证明△ABF∽△EBA，根据相似三角形的对应边的比相等即可证得．
（2）证明△ABF∽△EBA，根据相似三角形的对应边的比相等即可证得．
解答：
解：（1）∠BDC=∠BAC=∠ACB=∠ADB；
（2）连结AE，
∵AB=BC，
∴
=
，
∴∠E=∠CAB，
又∵∠ABF=∠EBA，
∴△ABF∽△EBA，
∴
=
，即AB2=BE•BF，
又∵AB=BC，
∴BC2=BE•BF．
解：（1）∠BDC=∠BAC=∠ACB=∠ADB；（2）连结AE，
∵AB=BC，
∴
 |
| AB |
|
| BC |
∴∠E=∠CAB，
又∵∠ABF=∠EBA，
∴△ABF∽△EBA，
∴
| BF |
| AB |
| AB |
| BE |
又∵AB=BC，
∴BC2=BE•BF．
点评：此题主要考查了圆周角定理和相似三角形的判定与性质，理解圆周角定理，证明△ABF∽△EBA是关键．
练习册系列答案
相关题目
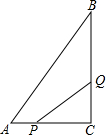如图所示，在△ABC中，∠C=90°，AC=6cm，BC=8cm，点P从点A出发沿边AC向点C以1cm/s的速度移动，点Q从C点出发沿CB边向点B以2cm/s的速度移动．如果P、Q同时出发，几秒钟后，可使△PCQ的面积为8平方厘米？
如图，已知E是AB边的中点，AC与ED相交于点F，且F是AC、DE的中点．求证：
如图：AC∥EF，AC=EF，AE=BD．求证：BC∥DF．