题目内容
 如图:AC∥EF,AC=EF,AE=BD.求证:BC∥DF.
如图:AC∥EF,AC=EF,AE=BD.求证:BC∥DF.考点:全等三角形的判定与性质
专题:证明题
分析:由平行可得∠A=∠FED,再结合线段相等可证明△ABC≌△EDF,可得∠CBA=∠D,可得BC∥DF.
解答:证明:∵AC∥EF,
∴∠A=∠FED,
∵AE=BD,
∴AE+EB=EB+BD,
即AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SAS),
∴∠CBA=∠D,
∴BC∥DF.
∴∠A=∠FED,
∵AE=BD,
∴AE+EB=EB+BD,
即AB=ED,
在△ABC和△EDF中,
|
∴△ABC≌△EDF(SAS),
∴∠CBA=∠D,
∴BC∥DF.
点评:本题主要考查全等三角形的判定和性质及平行线的性质和判定,掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
在-0.4217中用数字3替换其中的一个非零数字后,使所得的数最小,则被替换的数字是( )
| A、4 | B、2 | C、1 | D、7 |
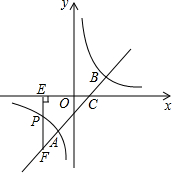 如图,直线y=x-1与反比例函数y=
如图,直线y=x-1与反比例函数y= 如图,四边形ABCD为等腰梯形,它的对称轴为y轴,A(-3,0),C(2,-2),则B、D两点的坐标分别是
如图,四边形ABCD为等腰梯形,它的对称轴为y轴,A(-3,0),C(2,-2),则B、D两点的坐标分别是 如图:AB⊥BD,ED⊥BD,AB=CD,AC=CE.求证:AC⊥CE.
如图:AB⊥BD,ED⊥BD,AB=CD,AC=CE.求证:AC⊥CE. 如图,已知AC、BD是圆内接四边形ABCD的两条对角线,且AB=BC,过B作一弦BE交AC于点F.
如图,已知AC、BD是圆内接四边形ABCD的两条对角线,且AB=BC,过B作一弦BE交AC于点F.