题目内容
(1)已知a=
-2,b=
+2,求
的值.
(2)已知(2m+2n+1)(2m+2n-1)=63,求m+n的值.
| 5 |
| 5 |
|
(2)已知(2m+2n+1)(2m+2n-1)=63,求m+n的值.
考点:二次根式的化简求值,换元法解一元二次方程
专题:计算题
分析:(1)先计算a-b与ab的值,再利用通分把
变形为
,然后利用整体代入的方法计算;
(2)设2m+2n=t,原方程变形为(t+1)(t-1)=63,再解关于t的一元二次方程,求出t的值,然后计算m+n的值.
|
|
(2)设2m+2n=t,原方程变形为(t+1)(t-1)=63,再解关于t的一元二次方程,求出t的值,然后计算m+n的值.
解答:解:(1)∵a=
-2,b=
+2,
∴a-b=-4,ab=5-4=1,
∴
=
=
=2;
(2)设2m+2n=t,
原方程变形为(t+1)(t-1)=63,
即t2=64,解得t1=8,t2=-8,
当t=8时,2m+2n=8,则m+n=4;
当t=-8时,2m+2n=-8,则m+n=-4.
| 5 |
| 5 |
∴a-b=-4,ab=5-4=1,
∴
|
|
|
(2)设2m+2n=t,
原方程变形为(t+1)(t-1)=63,
即t2=64,解得t1=8,t2=-8,
当t=8时,2m+2n=8,则m+n=4;
当t=-8时,2m+2n=-8,则m+n=-4.
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.也考查了换元法解方程.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
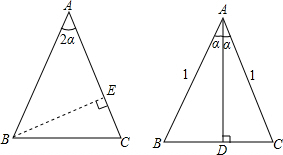 如图,在△ABC中,AB=AC=1,∠BAC=2α.请根据图中的提示,利用面积方法证明:sin2α=2sinα•cosα.
如图,在△ABC中,AB=AC=1,∠BAC=2α.请根据图中的提示,利用面积方法证明:sin2α=2sinα•cosα. 观察如图,用“>”或“<”填空.
观察如图,用“>”或“<”填空. 如图,四边形ABCD为等腰梯形,它的对称轴为y轴,A(-3,0),C(2,-2),则B、D两点的坐标分别是
如图,四边形ABCD为等腰梯形,它的对称轴为y轴,A(-3,0),C(2,-2),则B、D两点的坐标分别是 如图,已知AC、BD是圆内接四边形ABCD的两条对角线,且AB=BC,过B作一弦BE交AC于点F.
如图,已知AC、BD是圆内接四边形ABCD的两条对角线,且AB=BC,过B作一弦BE交AC于点F.