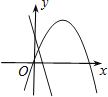题目内容
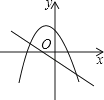
【题目】如图1，在平面直角坐标系中，抛物线y=﹣ 
x2+ 
x+3与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，抛物线的顶点为点E．
（1）判断△ABC的形状，并说明理由；
（2）经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一动点，当△PCD的面积最大时，Q从点P出发，先沿适当的路径运动到抛物线的对称轴上点M处，再沿垂直于抛物线对称轴的方向运动到y轴上的点N处，最后沿适当的路径运动到点A处停止．当点Q的运动路径最短时，求点N的坐标及点Q经过的最短路径的长；
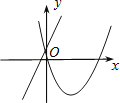
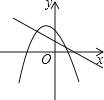
（3）如图2，平移抛物线，使抛物线的顶点E在射线AE上移动，点E平移后的对应点为点E′，点A的对应点为点A′，将△AOC绕点O顺时针旋转至△A1OC1的位置，点A，C的对应点分别为点A1 ， C1 ， 且点A1恰好落在AC上，连接C1A′，C1E′，△A′C1E′是否能为等腰三角形？若能，请求出所有符合条件的点E′的坐标；若不能，请说明理由．
【答案】
（1）
解：△ABC为直角三角形，
当y=0时，即﹣ 
x2+ 
x+3=0，
∴x1=﹣ 
，x2=3
∴A（﹣ ，0），B（3 ，0），
∴OA= ，OB=3 ，
当x=0时，y=3，
∴C（0，3），
∴OC=3，
根据勾股定理得，AC2=OB2+OC2=12，BC2=OB2+OC2=36，
∴AC2+BC2=48，
∵AB2=[3 ﹣（﹣ ）]2=48，
∴AC2+BC2=AB2，
∴△ABC是直角三角形
（2）
解：如图，
∵B（3 ，0），C（0，3），
∴直线BC解析式为y=﹣ 
x+3，
过点P作∥y轴，
设P（a，﹣ a2+ a+3），
∴G（a，﹣ a+3），
∴PG=﹣ a2+ a，
设点D的横坐标为xD，C点的横坐标为xC，
S△PCD= 
×（xD﹣xC）×PG=﹣ 
（a﹣ 
）2+ 
，
∵0＜a＜3 ，
∴当a= 时，S△PCD最大，此时点P（ ， 
），
将点P向左平移 个单位至P′，连接AP′，交y轴于点N，过点N作MN⊥抛物线对称轴于点M，
连接PM，点Q沿P→M→N→A，运动，所走的路径最短，即最短路径的长为PM+MN+NA的长，
∴P（ ， ）
∴P′（ 
， ），
∵点A（﹣ ，0），
∴直线AP′的解析式为y= 
x+ 
，
当x=0时，y= ，
∴N（0， ），
过点P′作P′H⊥x轴于点H，
∴AH= ，P′H= ，AP′= 
，
∴点Q运动得最短路径长为PM+MN+AN= + = 
；
（3）
解：在Rt△AOC中，
∵tan∠OAC= 
= ，
∴∠OAC=60°，
∵OA=OA1，
∴△OAA1为等边三角形，
∴∠AOA1=60°，
∴∠BOC1=30°，
∵OC1=OC=3，
∴C1（ ， 
），
∵点A（﹣ ，0），E（ ，4），
∴AE=2 
，
∴A′E′=AE=2 ，
∵直线AE的解析式为y= x+2，
设点E′（a， a+2），
∴A′（a﹣2 ， ﹣2）
∴C1E′2=（a﹣2 ）2+（ +2﹣ ）2= 
a2﹣ 
a+7，
C1A′2=（a﹣2 ﹣ ）2+（ ﹣2﹣ ）2= a2﹣ 
a+49，
①若C1A′=C1E′，则C1A′2=C1E′2
即： a2﹣ a+7= a2﹣ a+49，
∴a= ，
∴E′（ ，5），
②若A′C1=A′E′，
∴A′C12=A′E′2
即： a2﹣ a+49=28，
∴a1= 
，a2= 
，
∴E′（ ，7+ 
），或（ ，7﹣ ），
③若E′A′=E′C1，
∴E′A′2=E′C12
即： a2﹣ a+7=28，
∴a1= 
，a2= 
（舍），
∴E′（ ，3+ ），
即，符合条件的点E′（ ，5），（ ，7+ ），或（ ，7﹣ ），（ ，3+ ）
【解析】（1）先求出抛物线与x轴和y轴的交点坐标，再用勾股定理的逆定理判断出△ABC是直角三角形；（2）先求出S△PCD最大时，点P（ ， ），然后判断出所走的路径最短，即最短路径的长为PM+MN+NA的长，计算即可；（3）△A′C1E′是等腰三角形，分三种情况分别建立方程计算即可．此题是二次函数综合题，主要考查了函数极值的确定方法，等边三角形的判定和性质，勾股定理的逆定理，等腰三角形的性质，解本题的关键是分类讨论，也是解本题的难点．
【考点精析】解答此题的关键在于理解二次函数的最值的相关知识，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a，以及对勾股定理的逆定理的理解，了解如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．
