Question

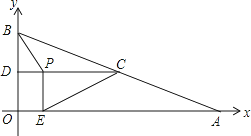
【题目】如图，已知直线l：y=﹣x，双曲线y= ，在l上取一点A（a，﹣a）（a＞0），过A作x轴的垂线交双曲线于点B，过B作y轴的垂线交l于点C，过C作x轴的垂线交双曲线于点D，过D作y轴的垂线交l于点E，此时E与A重合，并得到一个正方形ABCD，若原点O在正方形ABCD的对角线上且分这条对角线为1：2的两条线段，则a的值为 ．

Answer 1

【答案】 或
【解析】解：依照题意画出图形，如图所示．

∵点A的坐标为（a，﹣a）（a＞0），
∴点B（a， ）、点C（﹣ ， ）、点D（﹣ ，﹣a），
∴OA= = a，OC= = ．
又∵原点O分对角线AC为1：2的两条线段，
∴OA=2OC或OC=2OA，
即 a=2× 或 =2 a，
解得：a1= ，a2=﹣ （舍去），a3= ，a4=﹣ （舍去）．
所以答案是： 或 ．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．