题目内容
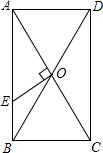 如图,在矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则BE的长为
如图,在矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则BE的长为考点:矩形的性质,三角形的面积,线段垂直平分线的性质,勾股定理
专题:
分析:首先连接EC,由题意可得OE为对角线AC的垂直平分线,可得CE=AE,S△AOE=S△COE=5,继而可得
AE•BC=10,则可求得AE的长,即EC的长,然后由勾股定理求得答案.
| 1 |
| 2 |
解答: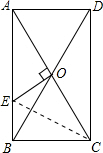 解:连接EC.
解:连接EC.
由题意可得,OE为对角线AC的垂直平分线,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10.
∴
AE•BC=10,
又∵BC=4,
∴AE=5,
∴EC=5.
在Rt△BCE中,由勾股定理得:BE=
=
=3.
故答案为:3.
 解:连接EC.
解:连接EC.由题意可得,OE为对角线AC的垂直平分线,
∴CE=AE,S△AOE=S△COE=5,
∴S△AEC=2S△AOE=10.
∴
| 1 |
| 2 |
又∵BC=4,
∴AE=5,
∴EC=5.
在Rt△BCE中,由勾股定理得:BE=
| EC2-BC2 |
| 52-42 |
故答案为:3.
点评:此题考查了矩形的性质、勾股定理以及三角形的面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目