题目内容
当m= 时，点P（2m-5，m-1）在二、四象限的角平分线上．
考点：点的坐标
专题：
分析：根据点P在二、四象限的角平分线上，让点P的横纵坐标相加得0即可求得m的值．
解答：解：∵点P（2m-5，m-1）在第二、四象限的夹角角平分线上，
∴2m-5+（m-1）=0，
解得：m=2．
故答案为：2．
∴2m-5+（m-1）=0，
解得：m=2．
故答案为：2．
点评：本题主要考查了点的坐标性质，利用第二、四象限的夹角平分线上的点的横纵坐标互为相反数得出是解题关键．
练习册系列答案
相关题目
如图：在△ABC中，∠BAD=∠B，∠C=∠ADC，∠BAC=60°，求∠DAC的度数．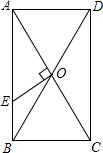
如图，在矩形ABCD的对角线AC，BD相交于点O，过点O作OE⊥AC交AB于E，若BC=4，△AOE的面积为5，则BE的长为