题目内容
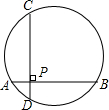 如图,AB、CD为弦,AB⊥CD于点P.求PA2+PB2+PC2+PD2的值.
如图,AB、CD为弦,AB⊥CD于点P.求PA2+PB2+PC2+PD2的值.考点:垂径定理,勾股定理
专题:计算题
分析:作OM⊥AB于M,ON⊥CD于N,如图,设⊙O的半径为r,根据垂径定理得AM=BM,CN=DN,再表示出PA=AM-PM=MB-PM,PB=PM+BM,PD=DN-PN=CN-PN,PC=PN+CN,所以PA2+PB2+PC2+PD2,整理得2(BM2+PM2+CN2+PN2),接着利用四边形OMPN为矩形得到PN=OM,PM=ON,则PA2+PB2+PC2+PD2=2(BM2+ON2+CN2+OM2),然后根据勾股定理得到BM2+OM2=OB2=r2,CN2+ON2=OC2=r2,于是PA2+PB2+PC2+PD2=2(r2+r2)=4r2.
解答:解:作OM⊥AB于M,ON⊥CD于N,如图,设⊙O的半径为r,
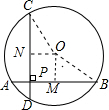 则AM=BM,CN=DN,
则AM=BM,CN=DN,
∵PA=AM-PM=MB-PM,PB=PM+BM,
PD=DN-PN=CN-PN,PC=PN+CN,
∴PA2+PB2+PC2+PD2=(MB-PM)2+(PM+BM)2+(CN-PN)2+(PN+CN)2=2(BM2+PM2+CN2+PN2),
∵AB⊥CD,
∴四边形OMPN为矩形,
∴PN=OM,PM=ON,
∴PA2+PB2+PC2+PD2=2(BM2+PM2+CN2+PN2)=2(BM2+ON2+CN2+OM2),
而BM2+OM2=OB2=r2,CN2+ON2=OC2=r2,
∴PA2+PB2+PC2+PD2=2(r2+r2)=4r2.
 则AM=BM,CN=DN,
则AM=BM,CN=DN,∵PA=AM-PM=MB-PM,PB=PM+BM,
PD=DN-PN=CN-PN,PC=PN+CN,
∴PA2+PB2+PC2+PD2=(MB-PM)2+(PM+BM)2+(CN-PN)2+(PN+CN)2=2(BM2+PM2+CN2+PN2),
∵AB⊥CD,
∴四边形OMPN为矩形,
∴PN=OM,PM=ON,
∴PA2+PB2+PC2+PD2=2(BM2+PM2+CN2+PN2)=2(BM2+ON2+CN2+OM2),
而BM2+OM2=OB2=r2,CN2+ON2=OC2=r2,
∴PA2+PB2+PC2+PD2=2(r2+r2)=4r2.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
相关题目
某环境检测中心关于2013年1月份第二周的空气质量报告中某项污染指数的数据如表所示,这组数据的众数是( )
| 检测时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 污染指数 | 21 | 22 | 21 | 24 | 20 | 22 | 21 |
| A、20 | B、21 | C、22 | D、24 |
在实数-
,
,
,-0.518,
,0.101001…中,无理数的个数有( )
| 21 |
| 7 |
| 8 |
| 3 | -8 |
| π |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
地球与太阳的平均距离大约为150000000km,这个数据用科学记数法表示正确的是( )
| A、1.5×107 |
| B、1.5×108 |
| C、15×108 |
| D、15×107 |
不等式组
的非负整数解有( )
|
| A、3个 | B、4个 | C、5个 | D、6个 |