题目内容
5.计算:(1)($\frac{3}{2}$-$\frac{1}{7}$)0+(-$\frac{1}{3}$)-2-(-1)2017
(2)已知:a、b、c为三角形的三边长,化简:|b+c-a|+|b-c-a|-|c-a-b|-|a-b+c|.
分析 (1)根据零指数幂以及负整数指数幂的运算法则计算即可;
(2)根据三角形的两边之和大于第三边,进而得到a,b和c之间的数量关系,即可化简.
解答 解:(1)($\frac{3}{2}$-$\frac{1}{7}$)0+(-$\frac{1}{3}$)-2-(-1)2017
=1+9+1
=11
(2)∵a、b、c为三角形的三边长,
∴b+c>a,a+c>b,a+b>c,a+c>b,
∴|b+c-a|+|b-c-a|-|c-a-b|-|a-b+c|
=b+c-a+a+c-b+c-a-b+b-a-c
=2c-2a
点评 本题考查的是三角形的三边关系和实数的运算,熟知三角形任意两边之和大于第三边,任意两边之差小于第三边是解答此题的关键.

练习册系列答案
相关题目
10.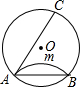 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
 如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )
如图,将⊙O沿弦AB折叠得到$\widehat{AmB}$所在圆的切线交⊙O于点C,若⊙O的半径为1,当AC取最大值时,则弦AB的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是垂线段最短.
如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段BN的长度,这样测量的依据是垂线段最短.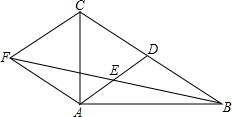 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
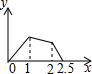
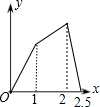
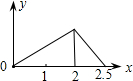
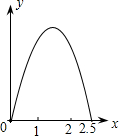
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.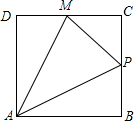 如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )
如图,在边长为1的正方形ABCD的边上有一点P按A→B→C→M的顺序运动,M是边CD上的中点,设点P经过的路程x为自变量,△APM的面积为y,则函数的大致图象是( )