题目内容
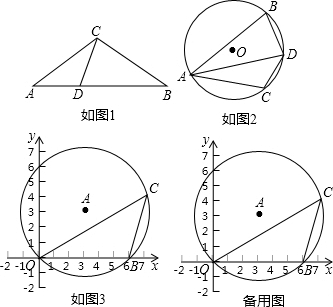
11. 如图,在E在线段AB上,分别以AB、BE为边长在AB的两侧作等边△ABC和等边△BDE.
如图,在E在线段AB上,分别以AB、BE为边长在AB的两侧作等边△ABC和等边△BDE.(1)连结AD、CE,求证:△ABD≌△CBE;
(2)延长CE交AD于F,求∠AFC的度数.
分析 (1)利用等边三角形的性质和全等三角形的判定定理SAS证得结论;
(2)利用(1)中全等三角形的对应角相等得到∠1=∠2.利用等边三角形的每一内角为60°和三角形内角和定理进行解答.
解答  (1)证明:∵△ABC和△BDE都是等边三角形,
(1)证明:∵△ABC和△BDE都是等边三角形,
∴∠ABD=∠CBE=60°,CB=AB,BD=BE,
在△ABD与△CBE中,
$\left\{\begin{array}{l}{BD=BE}\\{∠ABD=∠CBE}\\{AB=CB}\end{array}\right.$,
∴△ABD≌△CBE(SAS).
(2)解:由(1)知:△ABD≌△CBE,则∠1=∠2.
∵∠BAC=∠ACB=60°,
∴∠2+∠3=60°,
∴∠AFC=180°-∠BAC-(∠1+∠3)=180°-60°-(∠2+∠3)=60°,即∠AFC=60°.
点评 本题考查了全等三角形的判定与性质和等边三角形的性质.解题时,注意等边三角形的每一内角为60°是隐含在题中的已知条件.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
16.(1)$\sqrt{18}$×$\sqrt{\frac{1}{2}}$÷$\sqrt{3}$
(2)$\sqrt{8}$+2$\sqrt{3}$-($\sqrt{27}$-$\sqrt{2}$)
(2)$\sqrt{8}$+2$\sqrt{3}$-($\sqrt{27}$-$\sqrt{2}$)
20.关于点到直线的距离的四种说法正确的是( )
| A. | 连接直线外的点和直线上的点的线段叫做点到直线的距离 | |
| B. | 连接直线外的点和直线上的点的线段的长度叫做点到直线的距离 | |
| C. | 直线外一点到这条直线的垂线段叫做这点到直线的距离 | |
| D. | 直线外一点到这条直线的垂线段的长度叫做这点到直线的距离 |
1.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A. | 方差是8.02 | B. | 中位数是9 | C. | 众数是5 | D. | 极差是9 |