题目内容
6.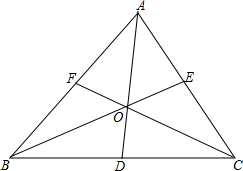 如图所示,在△ABC中,中线AD,BE,CF相交于点O.如果△ABC的面积为12cm2,(1)求△ABD的面积; (2)求△AFO,△BDO,△CEO的面积.
如图所示,在△ABC中,中线AD,BE,CF相交于点O.如果△ABC的面积为12cm2,(1)求△ABD的面积; (2)求△AFO,△BDO,△CEO的面积.
分析 (1)三角形的中线将三角形的面积等分成两份,从而求得△ABD的面积;
(2)根据重心的性质可以分别得到FO=$\frac{1}{3}$CF,OD=$\frac{1}{3}$AD,OE=$\frac{1}{3}$BE,根据S△ACF=S△ABD=S△BCE=$\frac{1}{2}$S△ABC从而求得△AFO,△BDO,△CEO的面积.
解答 解:(1)∵AD为△ABC的中线,
∴S△ABD=$\frac{1}{2}$S△ABC,
∵△ABC的面积为12cm2,
∴△ABD的面积为6cm2;
(2)由(1)可知S△ACF=S△ABD=S△BCE=$\frac{1}{2}$S△ABC=6cm2,
∵中线AD,BE,CF相交于点O,
∴FO=$\frac{1}{3}$CF,OD=$\frac{1}{3}$AD,OE=$\frac{1}{3}$BE,
∴S△AFO=$\frac{1}{3}$S△ACF=$\frac{1}{3}$×6=2cm2,S△BDO=$\frac{1}{3}$S△ABD=2cm2,S△CEO=$\frac{1}{3}$S△BCE=2cm2.
点评 本题考查了三角形的面积,三角形中线的性质以及三角形重心的性质,熟练掌握这些性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若一个数的倒数等于它本身,这样的数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
 如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?
如图,用钢筋做支架,要求BA,DC相交所成的锐角为32°,现测得∠BAC=∠DCA=115°,则这个支架符合设计要求吗?为什么?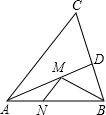 如图,在等腰△ABC中,AB=AC=13,BC=10,D是BC边上的中点,M、N分别是AD和AB上的动点.则BM+MN的最小值是$\frac{120}{13}$.
如图,在等腰△ABC中,AB=AC=13,BC=10,D是BC边上的中点,M、N分别是AD和AB上的动点.则BM+MN的最小值是$\frac{120}{13}$. a,b为有理数,且a+b,a-b在数轴上如图所示:
a,b为有理数,且a+b,a-b在数轴上如图所示: