题目内容
18. a,b为有理数,且a+b,a-b在数轴上如图所示:
a,b为有理数,且a+b,a-b在数轴上如图所示:(1)判断a,b的符号及a,b的大小关系;
(2)若x=|2a+b|-3|b|-|3-2a|+2|b-1|,求代数式x2-6x+9的值;
(3)若c为有理数,且$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$,ab+bc+ca=188,求代数式(a-b+c)2-abc的值.
分析 (1)由a+b<-3,a-b<3,可知a<0,b<0,且a>b;
(2)由(1)中a、b的关系化简得出x的数值,进一步代入求得答案即可;
(3)设$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$=k,得出a=3k,b=4k,c=5k,代入ab+bc+ca=188求得k的数值,得出a,b,c,进一步求得代数式的数值即可.
解答 解:(1)∵a+b<-3,a-b<3,
∴a<0,b<0,且a>b;
(2)∵x=|2a+b|-3|b|-|3-2a|+2|b-1|
=-2a-b+3b-3+2a-2b+2
=-1,
∴x2-6x+9=16;
(3)设$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$=k,
则a=3k,b=4k,c=5k,
∵ab+bc+ca=188,
∴12k2+20k2+15k2=188,
解得:k=±2,
则a=6,b=8,c=10或a=-6,b=-8,c=-10,
∴(a-b+c)2-abc=-416或544.
点评 此题考查代数式求值,数轴,绝对值及有理数的运算法则,注意代换方法的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.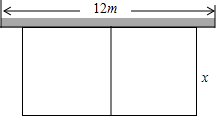 有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
 有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
有长24m的篱笆,一面利用长为12m的围墙围成如图所示中间隔有一道篱笆的矩形花圃.设花圃垂直于墙的一边长为xm,面积为Sm2.则S与x的函数关系式是S=(24-3x)x,x的取值范围为4≤x<8.
9.在Rt△ABC中,∠C=90°,点D是斜边AB的中点,若BC=6,CD=5,则cosB的值为( )
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
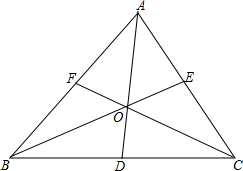 如图所示,在△ABC中,中线AD,BE,CF相交于点O.如果△ABC的面积为12cm2,(1)求△ABD的面积; (2)求△AFO,△BDO,△CEO的面积.
如图所示,在△ABC中,中线AD,BE,CF相交于点O.如果△ABC的面积为12cm2,(1)求△ABD的面积; (2)求△AFO,△BDO,△CEO的面积. 如图,在△ABC中,BC=5cm,边长为2cm的正方形DEFG的一边EF在BC上,点D在AB上,点G在AC上,求△ABC的面积.
如图,在△ABC中,BC=5cm,边长为2cm的正方形DEFG的一边EF在BC上,点D在AB上,点G在AC上,求△ABC的面积.