题目内容
11.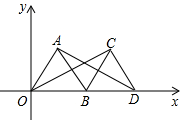 如图,在平面直角坐标系中,如图所示,△AOB是边长为2的等边三角形,将△AOB绕着点B按顺时针方向旋转得到△DCB,使得点D落在x轴的正半轴上,连接OC、AD.
如图,在平面直角坐标系中,如图所示,△AOB是边长为2的等边三角形,将△AOB绕着点B按顺时针方向旋转得到△DCB,使得点D落在x轴的正半轴上,连接OC、AD.(1)求证:OC=AD;
(2)求OC的长.
分析 (1)根据等边三角形的性质,可得OA=OB=AB=2,∠AOB=∠BAO=∠OBA=60°,根据旋转的性质,可得∠OBC=∠ABD,根据SAS,可得三角形全等,根据全等三角形的性质,可得答案;
(2)根据旋转的性质,可得BO=BC,∠DBC=∠BCD=60°,根据等腰三角形的性质,可得∠OCB的度数,根据勾股定理,可得答案.
解答 (1)证明:∵△AOB是边长为2的等边三角形,
∴OA=OB=AB=2,∠AOB=∠BAO=∠OBA=60°,
又△DCB是由△AOB绕着点B按顺时针方向旋转得到的,
∴△DCB也是边长为2的等边三角形,
∴∠OBA=∠CBD=60°,OB=AB,BC=BD,
又∠OBC=∠OBA+∠ABC=∠CBD+∠ABC=∠ABD,
在△OBC和△ABD中,
$\left\{\begin{array}{l}{OB=OA}\\{∠OBC=∠ABD}\\{BC=BD}\end{array}\right.$
∴△OBC≌△ABD(SAS),
∴OC=AD;
(2)解:∵△AOB与△BCD是边长为2的等边三角形,
∴BO=BC,∠DBC=∠BCD=60°,
∴∠BOC=∠BCO=30°,
∴∠OCD=90°.
∵OD=4,CD=2,
∴在Rt△OCD中,由勾股定理,得
OC=$\sqrt{O{D}^{2}-C{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 本题考查了旋转的性质,利用旋转得出∠OBC=∠ABD是解题关键,又利用了全等三角形的判定与性质.

练习册系列答案
相关题目
6.下列方程中,属于一元二次方程的是( )
| A. | x2-$\frac{1}{x}$=1 | B. | x2+y=2 | C. | $\sqrt{2}$x2=2 | D. | x+5=-7 |
1.能把一个三角形分成面积相等的两部分的是该三角形的一条( )
| A. | 高线 | B. | 角平分线 | C. | 中线 | D. | 边的垂直平分线 |
 定理:等腰三角形的两个底角相等(简称“等边对等角”).
定理:等腰三角形的两个底角相等(简称“等边对等角”).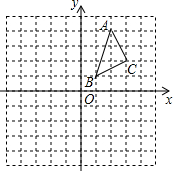 如图,在平面直角坐标系中,A(2,4),B(1,1),C(3,2).
如图,在平面直角坐标系中,A(2,4),B(1,1),C(3,2).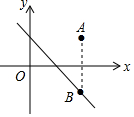 如图,在平面直角坐标系中点A(2,m)在第-象限,若点A关于x轴的对称点B在直线y=-x+1上,求m的值.
如图,在平面直角坐标系中点A(2,m)在第-象限,若点A关于x轴的对称点B在直线y=-x+1上,求m的值.