题目内容
19.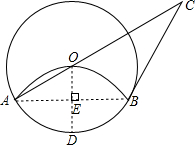 如图,将圆形纸片沿弦AB折叠后,圆弧恰好能经过圆心O,⊙O的切线BC与AO延长线交于点C.
如图,将圆形纸片沿弦AB折叠后,圆弧恰好能经过圆心O,⊙O的切线BC与AO延长线交于点C.(1)若⊙O半径为6cm,用扇形OAB围成一个圆锥的侧面,求这个圆锥的底面圆半径.
(2)求证:AB=BC.
分析 (1)过O作OD⊥AB于E,交⊙O于D,根据题意OE=$\frac{1}{2}$OA,得出∠OAE=30°,∠AOE=60°,从而求得∠AOB=2∠AOE=120°,根据弧长公式求得弧AB的长,然后根据圆锥的底面周长等于弧长得出2πr=4π,即可求得这个圆锥的底面圆半径;
(2)连接OB,根据切线的性质得出∠OBC=90°,根据三角形外角的性质得出∠C=30°,从而得出∠BAC=∠C,根据等角对等边即可证得结论.
解答 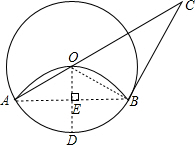 解:(1)设圆锥的底面圆半径为r,
解:(1)设圆锥的底面圆半径为r,
过O作OD⊥AB于E,交⊙O于D,连接OB,
有折叠可得 OE=$\frac{1}{2}$OD,
∵OD=OA,
∴OE=$\frac{1}{2}$OA,
∴在Rt△AOE中∠OAE=30°,则∠AOE=60°,
∵OD⊥AB,
∴∠AOB=2∠AOE=120°,
∴弧AB的长为:$\frac{120×π×6}{180}$=4π,
∴2πr=4π,
∴r=2;
(2)∵∠AOB=120°,
∴∠BOC=60°,
∵BC是⊙O的切线,
∴∠CBO=90°
∴∠C=30°,
∴∠OAE=∠C,
∴AB=BC.
点评 本题考查了折叠的性质,垂径定理,弧长的计算,切线的性质以及等腰三角形的判定和性质,找出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
10.式子$\sqrt{1-x}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x≥-1 | D. | x≤-1 |
7.下列计算错误的是( )
| A. | $1÷6×\frac{1}{6}=\frac{1}{36}$ | B. | (-2)-2=4 | C. | $\frac{1}{3}-2-(-2\frac{1}{3})=\frac{2}{3}$ | D. | 20150=1 |
4.为了控制房价,最近很多城市出台了房产购买限制措施,假设某人购买某处房子原来需支付首付款30%,即27万元,现在按照新规定首付款必须不低于50%,则这个人按照新规定至少支付首付款( )
| A. | 13.5万元 | B. | 45万元 | C. | 54万元 | D. | 100万元 |
11.下列运算正确的是( )
| A. | 3a+2b=5ab | B. | (3a)3=9a3 | C. | a3•a4=a7 | D. | a4+a3=a7 |
9.2016年1月5日,河北外国语学院举行“我说我校训”大学生演讲比赛,参赛选手共有12名.梦梦根据比赛中七位评委所给的某位参赛选手的分数制作了如下表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
| 众数 | 中位数 | 平均数 | 方差 |
| 9.2 | 9.1 | 9.1 | 0.2 |
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
 如图,Rt△ABC中∠A=90°,∠C=30°,BD平分∠ABC且与AC边交于点D,AD=2,则点D到边BC的距离是2.
如图,Rt△ABC中∠A=90°,∠C=30°,BD平分∠ABC且与AC边交于点D,AD=2,则点D到边BC的距离是2.