题目内容
若二次函数y=x2-ax+9的图象的顶点在坐标轴上,则a的值为 .
考点:二次函数的性质
专题:
分析:可利用顶点坐标公式求得顶点坐标,当顶点在x轴上时可知其最小值为0,当顶点在y轴上时可知其对称轴为0,可分别求得a的值.
解答:解:∵y=x2-ax+9,
∴其对称轴为x=
,最小值为9-
,
∴其顶点坐标为(
,9-
),
当顶点在x轴上时,则9-
=0,解得a=±6,
当顶点在y轴上时,则
=0,解得a=0,
故答案为:0或6或-6.
∴其对称轴为x=
| a |
| 2 |
| a2 |
| 4 |
∴其顶点坐标为(
| a |
| 2 |
| a2 |
| 4 |
当顶点在x轴上时,则9-
| a2 |
| 4 |
当顶点在y轴上时,则
| a |
| 2 |
故答案为:0或6或-6.
点评:本题主要考查二次函数的顶点坐标,掌握二次函数的顶点在坐标轴上的条件是解题的关键.

练习册系列答案
相关题目
下列四个图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
在⊙O中,弦AB所对的圆心角是40°,弦AB所对的圆周角是( )
| A、20° |
| B、80° |
| C、20°或160° |
| D、80°或100° |
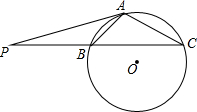 如图,P、B、C三点共线,⊙O经过B、C两点,A是⊙O上一点,连接PA,且∠PAB=∠C,PA=5,PB=3.
如图,P、B、C三点共线,⊙O经过B、C两点,A是⊙O上一点,连接PA,且∠PAB=∠C,PA=5,PB=3.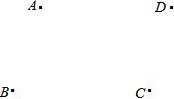 如图,已知A,B,C,D四个点,请按要求画图:
如图,已知A,B,C,D四个点,请按要求画图: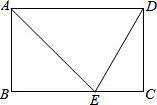 已知在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求证矩形的周长及对角线的长.
已知在矩形ABCD中,AE平分∠BAD,交BC于点E,ED=5,EC=3,求证矩形的周长及对角线的长.