题目内容
17.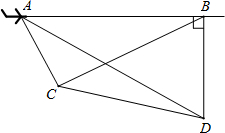 如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.
如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.
分析 根据题目中的俯角可以求出∠BAC=60°,∠ABC=30°,∠BAD=30°,进而得到∠ACB=90°,利用AB=6千米求得BC的长,然后求得CD两点间的水平距离,进而求得C、D之间的距离.
解答 解:∵飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°,
到B处时,往后测得山头C的俯角为30°,
∴∠BAC=60°,∠ABC=30°,∠BAD=30°,
∴∠ACB=180°-∠ABC-∠BAC=180°-30°-60°=90°,即△ABC为直角三角形,
∵AB=200×60=12000米=12千米,
∴BC=AB•cos30°=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$(千米).
Rt△ABD中,BD=AB•tan30°=12×$\frac{\sqrt{3}}{3}$=4$\sqrt{3}$(千米),
作CE⊥BD于E点,
∵AB⊥BD,∠ABC=30°,∴∠CBE=60°,
则BE=BC•cos60°=6$\sqrt{3}$×$\frac{1}{2}$=3$\sqrt{3}$,DE=BD-BE=4$\sqrt{3}$-3$\sqrt{3}$=$\sqrt{3}$,CE=BC•sin60°=6$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=9,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{3+81}$=2$\sqrt{21}$(千米).
∴山头C、D之间的距离2$\sqrt{21}$千米.
点评 本题考查了利用仰俯角问题解直角三角形的知识,解决此类题目的关键是正确的将仰俯角转化为直角三角形的内角并用解直角三角形的知识解答即可.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
5.下列运算中,正确的是( )
| A. | a3+a3=a6 | B. | a3•a2=a5 | C. | a3-a2=a | D. | a3•a3=a9 |
12.在△ABC中,AC=9,BC=12,AB=15,则点C到AB的距离是( )
| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{15}{2}$ |
6.要使算式“-1□1”的结果最小,在“□”中应填的运算符号是( )
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
 按照如图所示的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,那么a+b=4.
按照如图所示的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,那么a+b=4.