题目内容
12.在△ABC中,AC=9,BC=12,AB=15,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{15}{2}$ |
分析 利用勾股定理逆定理可证明∠C=90°,设点C到AB的距离是h,利用直角三角形的面积可得$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•h,再解即可.
解答 解:∵92+122=152,
∴AC2+BC2=AB2,
∴∠C=90°,
设点C到AB的距离是h,
$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•h,
解得:h=$\frac{36}{5}$.
故选:A.
点评 此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
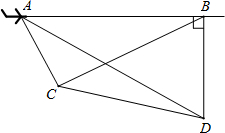 如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离.
如图,一架飞机以200米/秒的速度由A向B沿水平直线方向飞行,在航线AB的下方有两个山头C、D,飞机在A处时,测得山头C、D在飞机的前方,俯角分别为60°和30°.飞机飞行1分钟后到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.求山头C、D之间的距离. 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠1,∠2的度数,并说明理由.
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,求∠1,∠2的度数,并说明理由.