题目内容
解方程：x（2x+1）=8x-3．
解：去括号，得：2x2+x=8x-3，
移项，得：2x2+x-8x+3=0
合并同类项，得：2x2-7x+3=0，
∴（2x-1）（x-3）=0，
∴2x-1=0或 x-3=0，
∴
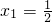，x2=3．
分析：运用因式分解法将原式分解因式，即可得出答案．
点评：本题主要考查了因式分解法解一元二次方程，根据已知将原式分解为两式相乘等于0是解决问题的关键．
移项，得：2x2+x-8x+3=0
合并同类项，得：2x2-7x+3=0，
∴（2x-1）（x-3）=0，
∴2x-1=0或 x-3=0，
∴
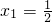，x2=3．分析：运用因式分解法将原式分解因式，即可得出答案．
点评：本题主要考查了因式分解法解一元二次方程，根据已知将原式分解为两式相乘等于0是解决问题的关键．
练习册系列答案
相关题目