题目内容
5. 如图,在平行四边形ABCD中,点E是AD边的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$.
如图,在平行四边形ABCD中,点E是AD边的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$.(1)试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{CE}$,那么$\overrightarrow{CE}$=-$\overrightarrow{b}$-$\overrightarrow{a}$;
(2)在图中求作:$\overrightarrow{BA}$-$\overrightarrow{AE}$.
(保留作图痕迹,不要求写作法,写出结果)
分析 (1)如图,过点E作EF∥AB,则点F是BC的中点,所以$\overrightarrow{EF}$=$\overrightarrow{AB}$,$\overrightarrow{FC}$=$\overrightarrow{AE}$,然后由三角形法则来求$\overrightarrow{CE}$;
(2)连接BE.由$\overrightarrow{BE}$=$\overrightarrow{BA}$+$\overrightarrow{AE}$,可得$\overrightarrow{BE}$-$\overrightarrow{AE}$=$\overrightarrow{BA}$.向量$\overrightarrow{BA}$即为所求;
解答 解:(1)如图,过点E作EF∥AB,则点F是BC的中点,所以$\overrightarrow{EF}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{FC}$=$\overrightarrow{AE}$=$\overrightarrow{b}$,
则$\overrightarrow{CE}$=$\overrightarrow{CF}$+$\overrightarrow{FE}$=-$\overrightarrow{b}$-$\overrightarrow{a}$.
(2) 连接BE.
连接BE.
∵$\overrightarrow{BE}$=$\overrightarrow{BA}$+$\overrightarrow{AE}$,
∴$\overrightarrow{BE}$-$\overrightarrow{AE}$=$\overrightarrow{BA}$.
∴向量$\overrightarrow{BA}$即为所求.
点评 本题考查平面向量、平行四边形的性质、三角形法则等知识,解题的关键是灵活运用三角形法则解决问题,属于中考基础题.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案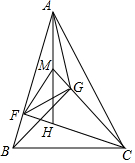 如图,△ABC为锐角三角形,CF⊥AB于F,H为△ABC的垂心.M为AH的中点,点G在线段CM上,且CG⊥GB.
如图,△ABC为锐角三角形,CF⊥AB于F,H为△ABC的垂心.M为AH的中点,点G在线段CM上,且CG⊥GB. 解不等式2x+1≥$\frac{8x-1}{3}$,并把它的解集在数轴上表示出来.
解不等式2x+1≥$\frac{8x-1}{3}$,并把它的解集在数轴上表示出来.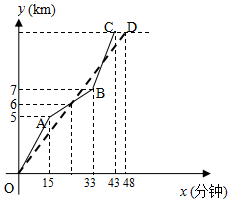 如图表示两名选手在一次自行车越野赛中,路程y(km)随时间x(分)变化的图象(全程),根据图象回答以下问题:
如图表示两名选手在一次自行车越野赛中,路程y(km)随时间x(分)变化的图象(全程),根据图象回答以下问题: