题目内容
 反比例函数y1、y2在第一象限的图象如图所示,已知y1=
反比例函数y1、y2在第一象限的图象如图所示,已知y1=| 4 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:设y2=
,根据反比例函数xy=k(k≠0)系数k的几何意义得到S△OAC=
×4=2,S△OBC=
k2,由S△AOB=2得到
k2-2=2,然后解方程即可.
| k2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设y2=
,
∵AB∥x轴,
∴S△OAC=
×4=2,S△OBC=
k2,
∴S△AOB=
k2-2=2,
∴k2=8,
∴y2的解析式是y2=
故答案为
.
| k2 |
| x |
∵AB∥x轴,
∴S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AOB=
| 1 |
| 2 |
∴k2=8,
∴y2的解析式是y2=
| 8 |
| x |
故答案为
| 8 |
| x |
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |
| k |
| x |

练习册系列答案
相关题目
下列计算中正确的是( )
| A、(π-3.14)0=1 | |||
B、-
| |||
| C、(-3a-2)(3a-2)=9a2-4 | |||
D、
|
苏州地铁二号线于2013年12月28日投入运营,二号线是苏州轨道交通线网的南北向骨干线路,线路全长26.557公里,共设22座车站,也是迄今为止苏州市投资规模最大的城市建设工程,工程总投资156亿元,总工期4年半.156亿用科学记数法表示为( )
| A、1.56×108 |
| B、1.56×109 |
| C、1.56×1010 |
| D、1.56×1011 |

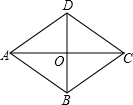 已知菱形ABCD边长为5,两条对角线AC,BD相交于O,已知OA,OB的长是关于x的方程x2+(2m-1)x+m2+3=0两根,则m=
已知菱形ABCD边长为5,两条对角线AC,BD相交于O,已知OA,OB的长是关于x的方程x2+(2m-1)x+m2+3=0两根,则m=