Question

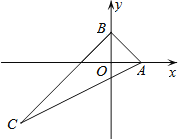
【题目】如图，△ABC在平面直角坐标系中，点A、B分别在x轴和y轴上，且OA＝OB，边AC所在直线解析式为y＝x﹣，若△ABC的内心在y轴上，则tan∠ACB的值为（　　）

A.B.C.D.

Answer 1

【答案】B

【解析】

△ABO是等腰直角三角形，然后根据△ABC的内心在y轴上，则BO是∠ABC的平分线，△ABC是直角三角形，求得BC的解析式，进而求得BC的长，然后根据三角函数的定义求解．

在y＝x﹣中，令y＝0，则x﹣＝0，解得x＝1，

∵OA＝OB，

∴B的坐标是（0，1），AB＝，△OAB是等腰直角三角形．

∴∠ABO=45°

∵△ABC的内心在y轴上，

∴∠ABC＝2∠ABO＝90°，即△ABC是直角三角形，

设BC的解析式是y＝x+c，

则把B（0，1）代入得c＝1，

则BC的解析式是y＝x+1，

根据题意得：，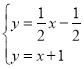

解得：，

即C的坐标是（﹣3，﹣2）．

∵B（0，1）

则BC＝，

则．

故选：B．