题目内容
16.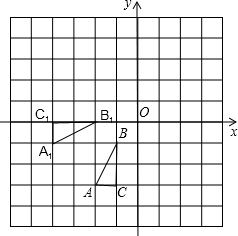 如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.
如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.(1)△ABC与△A1B1C1关于某条直线m对称,画出对称轴m.
(2)画出△A1B1C1绕原点O顺时针旋转90°所得的△A2B2C2.此时点A2的坐标为(1,4).求出点A1旋转到点A2的路径长.(结果保留根号)
分析 (1)直接利用轴对称图形的性质结合网格得出对称轴m;
(2)利用旋转的性质得出对应点位置进而得出答案,再利用弧长公式求出点A1旋转到点A2的路径长.
解答  解:(1)如图所示:直线m即为所求;
解:(1)如图所示:直线m即为所求;
(2)如图所示:△A2B2C2,即为所求,点A2的坐标为:(1,4),
点A1旋转到点A2的路径长为:$\frac{90π×\sqrt{17}}{180}$=$\frac{\sqrt{17}π}{2}$.
故答案为:$\frac{\sqrt{17}π}{2}$.
点评 此题主要考查了轴对称变换以及旋转变换、弧长公式等知识,根据题意得出对应点位置是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.地球的表面积约为510000000km2,将510000000用科学记数法表示为( )
| A. | 0.51×109 | B. | 5.1×109 | C. | 5.1×108 | D. | 0.51×107 |
5.将2.05×10-3用小数表示为( )
| A. | 0.000205 | B. | 0.0205 | C. | 0.00205 | D. | -0.00205 |
6.若关于x的一元二次方程4x2-4x+c=0有两个相等实数根,则c的值是( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |
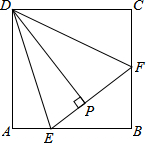 如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.
如图,在正方形ABCD中,E、F分别是AB、BC上的点,且∠EDF=45°,DP⊥EF于点P,求证:DP=DA.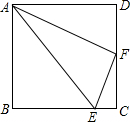 已知,如图,在正方形ABCD中,F是边CD的中点,点E在BC上,且AE=AD+CE.
已知,如图,在正方形ABCD中,F是边CD的中点,点E在BC上,且AE=AD+CE.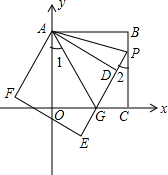 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.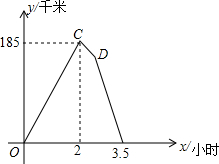 下面的图象反映的过程是:
下面的图象反映的过程是: