题目内容
在△ABC中,∠BAC=α.
(1)如图1,∠ABC与∠ACB的角平分线交于O,求∠BOC;
(2)如图2,∠MBC的角平分线与∠NCB的角平分线交于Q,求∠BQC.

(1)如图1,∠ABC与∠ACB的角平分线交于O,求∠BOC;
(2)如图2,∠MBC的角平分线与∠NCB的角平分线交于Q,求∠BQC.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)求出∠ABC+∠ACB的度数,根据平分线的定义得出∠OBC=
∠ABC,∠OCB=
∠ACB,求出∠OBC+∠OCB的度数,根据三角形内角和定理求出即可;
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形的外角性质分别表示出∠MBC与∠BCN,再根据角平分线的性质可求得∠CBQ+∠BCQ,最后根据三角形内角和定理即可求解.
解答:解:(1)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=
×(180°-α)=90°-
α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°
α)=90°+
α;
(2)∵∠MBC=∠A+∠ACB,∠BCN=∠ABC+∠A
∴∠MBC+∠BCN=∠A+∠ABC+∠ACB+∠A=180°+∠A
∵BE,CQ分别为△ABC的外角∠MBC,∠NCB的角平分线
∴∠CBQ+∠BCQ=
(180°+∠A)
∴∠BQC=180°-(∠CBQ+∠BCQ)=90°-
∠A=90°-
α.
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵∠MBC=∠A+∠ACB,∠BCN=∠ABC+∠A
∴∠MBC+∠BCN=∠A+∠ABC+∠ACB+∠A=180°+∠A
∵BE,CQ分别为△ABC的外角∠MBC,∠NCB的角平分线
∴∠CBQ+∠BCQ=
| 1 |
| 2 |
∴∠BQC=180°-(∠CBQ+∠BCQ)=90°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
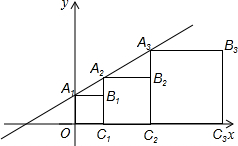 彼此相似的正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(
彼此相似的正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(