题目内容
8.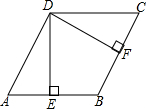 如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F,在不添加其他辅助线的情况下,请你找出图中所有的全等三角形,并证明你的结论.
如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F,在不添加其他辅助线的情况下,请你找出图中所有的全等三角形,并证明你的结论.
分析 先利用菱形的性质可求出一组对应角相等,一组对应边相等,再结合已知条件中的垂直条件,又可得一组对应角相等,从而利用AAS可证两个三角形全等.
解答 解:图中所有的全等三角形只有△ADE≌△DCF,
证明如下:
∵四边形ABCD是菱形,
∴∠A=∠C,AD=CD,
又∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠A=∠C}\\{∠AED=∠CFD}\\{AD=CD}\end{array}\right.$
∴△ADE≌△CDF(AAS).
点评 本题考查了平行四边形的性质,全等三角形的判定和性质以及菱形的判定方法,解题的关键是熟练掌握各种图形的判定和性质.

练习册系列答案
相关题目
16.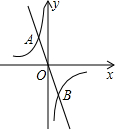 如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )
 如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )
如图,函数y1=$\frac{{k}_{1}}{x}$(k1≠0)与y2=k2x(k2≠0)的图象Ox交于A、B两点,且A(-1,3).若y1<y2,则x的取值范围是( )| A. | -1<x<0 | B. | x<-1或0<x<1 | C. | -1<x<1 | D. | -1<x<0或x>1 |
20.某校在七年级设立了六个课外兴趣小组,每个参加者只能参加一个兴趣小组,下面是六个兴趣小组不完整的频数分布直方图和扇形统计图.根据图中信息,可得下列结论不正确的是( )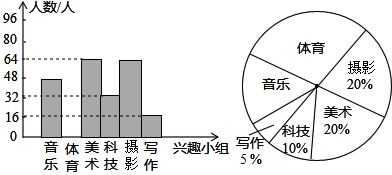

| A. | 七年级共有320人参加了兴趣小组 | |
| B. | 体育兴趣小组对应扇形圆心角的度数为96° | |
| C. | 各小组人数组成的数据的众数是64 | |
| D. | 各小组人数组成的数据的中位数是56 |
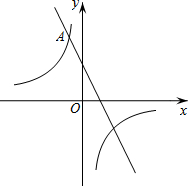 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).