题目内容
如图，在△ABO中，OA=OB边的中点，C是AB的中点，⊙O过点C，且与OA交于点E，与OB交于点F，连接CE、CF，点M在⊙O上，连接EM、FM．（1）求证：AB是⊙O的切线；
（2）若∠AOB=∠ECF，求∠M的度数．
考点：切线的判定
专题：
分析：（1）根据等腰三角形的性质求得OC⊥AB，根据切线的判定定理就可证得结论；
（2）根据圆内接四边形的性质得出∠M+∠ECF=180°，进而求得∠M+∠AOB=180°，根据圆心角、圆周角的性质得出∠AOB=2∠M，就可求得∠M的值．
（2）根据圆内接四边形的性质得出∠M+∠ECF=180°，进而求得∠M+∠AOB=180°，根据圆心角、圆周角的性质得出∠AOB=2∠M，就可求得∠M的值．
解答：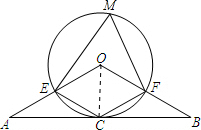
解：（1）连接OC，
∵在△ABO中，OA=OB，C是AB的中点，
∴OC⊥AB，
∴AB是⊙O的切线；
（2）∵∠M+∠ECF=180°，∠AOB=∠ECF，
∴∠M+∠AOB=180°，
∵∠AOB=2∠M，
∴3∠M=180°，
∴∠M=60°．
解：（1）连接OC，∵在△ABO中，OA=OB，C是AB的中点，
∴OC⊥AB，
∴AB是⊙O的切线；
（2）∵∠M+∠ECF=180°，∠AOB=∠ECF，
∴∠M+∠AOB=180°，
∵∠AOB=2∠M，
∴3∠M=180°，
∴∠M=60°．
点评：本题考查了等腰三角形的性质，切线的判定，圆心角、圆周角的性质等，熟练掌握性质和定理是解题的关键．
练习册系列答案
相关题目
