题目内容
 如图,OB、OD分别平分∠AOC、∠COE,若∠BOD=75°,则∠AOE等于( )
如图,OB、OD分别平分∠AOC、∠COE,若∠BOD=75°,则∠AOE等于( )| A、75° | B、100° |
| C、125° | D、150° |
考点:角平分线的定义
专题:
分析:首先根据角平分线的性质可得∠EOC=2∠DOC,∠AOC=2∠BOC,进而得到∠AOE=2∠BOD,从而得到答案.
解答:解:∵OB、OD分别平分∠AOC、∠COE,
∴∠EOC=2∠DOC,∠AOC=2∠BOC,
∵∠BOD=75°,
∴∠AOE=2∠DOC+2∠COB=2(∠DOC+∠BOC)=2∠BOD=150°,
故选:D.
∴∠EOC=2∠DOC,∠AOC=2∠BOC,
∵∠BOD=75°,
∴∠AOE=2∠DOC+2∠COB=2(∠DOC+∠BOC)=2∠BOD=150°,
故选:D.
点评:此题主要考查了角平分线的性质,关键是掌握从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
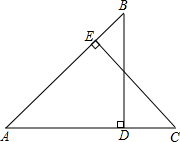 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,AD=AE.下列方法中,可以直接判断△ADB≌△AEC的是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
在△ABC中,∠C=90°,若tanB=
,则sinA=( )
| 5 |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
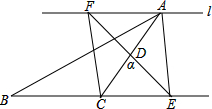 如图,在△ABC中∠ACB=90°,D是AC的中点,过点A的直线l∥BC,将直线AC绕点D逆时针旋转(旋转角α<∠ACB),分别交直线l于点F与BC的延长线交于点E,连接AE、CF.
如图,在△ABC中∠ACB=90°,D是AC的中点,过点A的直线l∥BC,将直线AC绕点D逆时针旋转(旋转角α<∠ACB),分别交直线l于点F与BC的延长线交于点E,连接AE、CF. 反比例函数y=
反比例函数y=



 已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.
已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.